
問題
単振動する一様な外場に揺すぶられる質点の運動を考えます。質点の質量を  単位、そして外力の振幅を
単位、そして外力の振幅を  単位,周期を
単位,周期を  単位とします。この時、質点の運動方程式は
単位とします。この時、質点の運動方程式は
となります:上付きドットは時間  微分を表します。初め 質点は一点
微分を表します。初め 質点は一点  に固定されていて、時刻
に固定されていて、時刻  に自由になるとします。すなわち
に自由になるとします。すなわち
ゆえ運動方程式を時間積分して
を得ます。ここで、運動エネルギー  は
は
ですが、このうち時間変化する項の時間平均  は
は
となり、時刻  に依りません。
に依りません。 は ポンデロモーティブエネルギーと呼ばれます。
は ポンデロモーティブエネルギーと呼ばれます。
さて、質点は外場に揺さぶられて  のオーダーの運動エネルギー
のオーダーの運動エネルギー  を得ますが、元の位置
を得ますが、元の位置  に戻った時の
に戻った時の  の取り得る最大の値は
の取り得る最大の値は  であることが知られています。この
であることが知られています。この  という数字がどの様にして出てきたのか以前から気になっていましたので、今回はこの計算に取り組んでみました
という数字がどの様にして出てきたのか以前から気になっていましたので、今回はこの計算に取り組んでみました
解くべき式
質点が元の位置  に戻る時刻を
に戻る時刻を  とおくと、
とおくと、
より
この式は、 と
と  で接し,
で接し, で交叉する直線の方程式です。下図1のように、
で交叉する直線の方程式です。下図1のように、 を決めると グラフから
を決めると グラフから  を求めることができます
を求めることができます
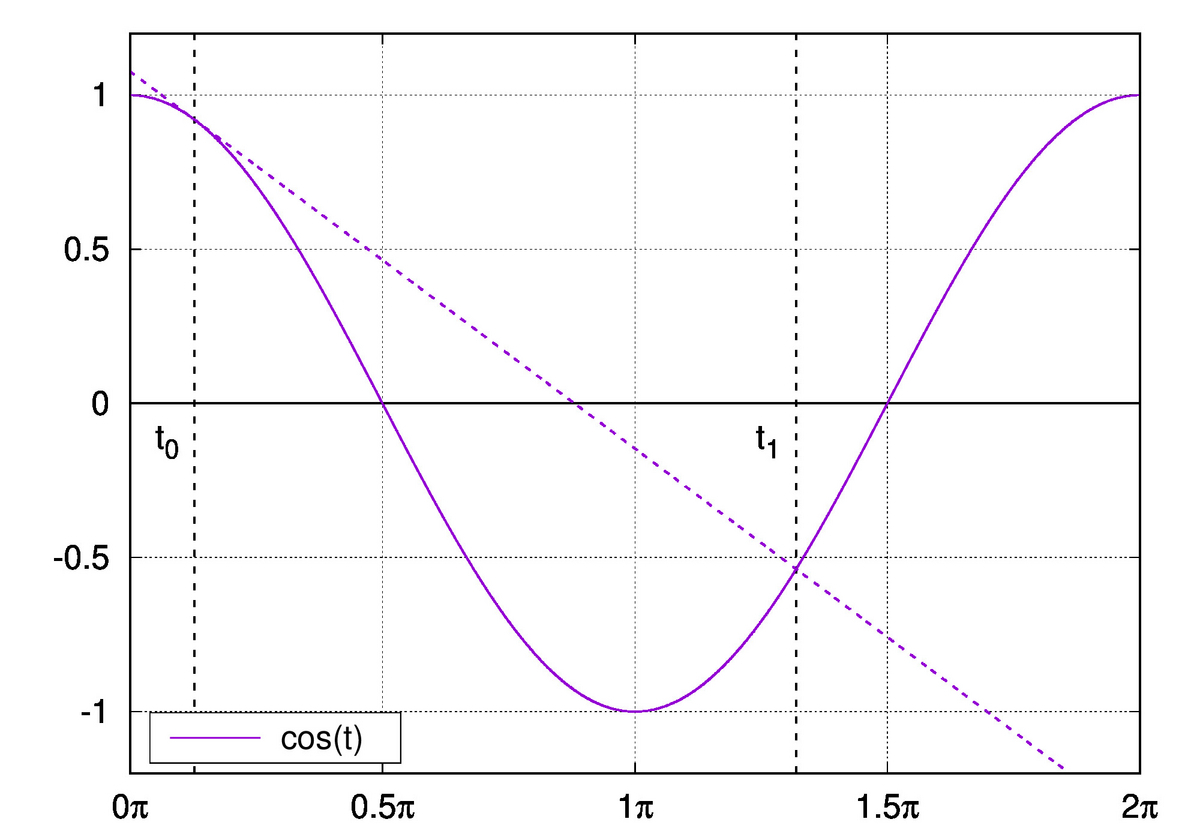 図1
図1  から
から  を求める
を求める
図から分かる通り、 の場合のみ接線は
の場合のみ接線は  に交点を持ち、質点が元の位置に戻ります。
に交点を持ち、質点が元の位置に戻ります。
さて、 が決まれば、速度は
が決まれば、速度は
と与えられます。そこで、当面の目標は 速さ  を最大にするような
を最大にするような  の条件式を導くことです。このような条件付き極値問題は、例えばラグランジュの未定乗数法で機械的に解くことができます。未定乗数を
の条件式を導くことです。このような条件付き極値問題は、例えばラグランジュの未定乗数法で機械的に解くことができます。未定乗数を  とおけば、ラグランジュ関数は
とおけば、ラグランジュ関数は
と書けます。そこで、 についての偏微係数をゼロとして条件式を得ます
についての偏微係数をゼロとして条件式を得ます
第1式から  となり、これを第2式に代入し整理して
となり、これを第2式に代入し整理して
を得ます。この式は、 と
と  で接し、
で接し、 で交叉する直線の方程式です。下図2のように、
で交叉する直線の方程式です。下図2のように、 が定まると グラフから
が定まると グラフから  を最大にする
を最大にする  の候補
の候補  を求めることができます
を求めることができます
 図2
図2  から
から  を求める
を求める
まとめますと、 を決めると
を決めると  の
の  での接線を描いて
での接線を描いて  が求まり、さらに
が求まり、さらに  の
の  での接線を描いて
での接線を描いて  が求まります。結局、
が求まります。結局、 となるように
となるように  を決めれば良いことになります。この時、グラフは下図3のようになるでしょう
を決めれば良いことになります。この時、グラフは下図3のようになるでしょう
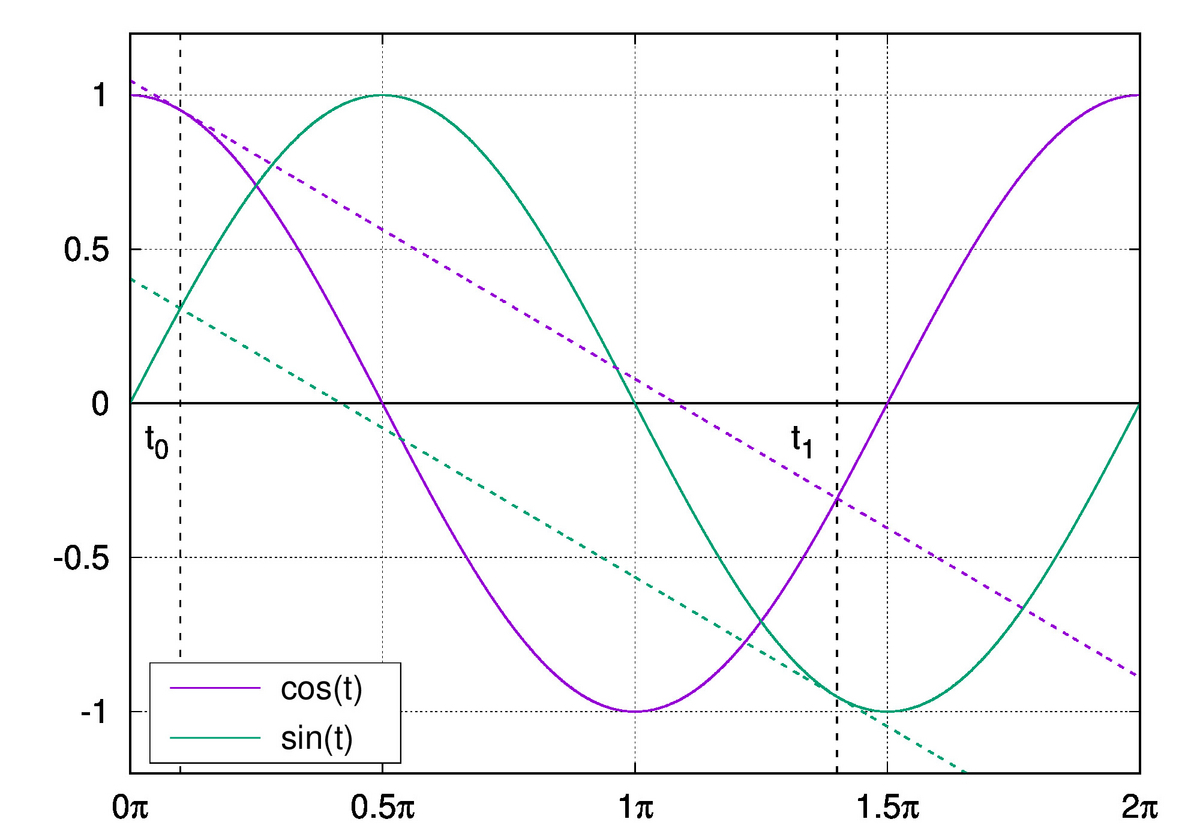 図3
図3  のとき
のとき
図3で、紫線と緑線は  を中心に
を中心に  回転させると互いに一致します。ゆえ
回転させると互いに一致します。ゆえ
です。そこで、 の条件式から
の条件式から  を消去して整理しますと
を消去して整理しますと
を得ます。この式から  を求めると、
を求めると、 での運動エネルギーの最大値
での運動エネルギーの最大値
が計算でき、
となるはずです
計算
得られた  の条件式は、恐らく
の条件式は、恐らく  について解析的に解くことができません。そこで、ニュートン・ラフソン法などを使って数値的に解くと
について解析的に解くことができません。そこで、ニュートン・ラフソン法などを使って数値的に解くと
を得ます。これで話を終えてしまうのは ちょっと物足りない気がしますので、悪あがきして  の近似式を求めてみようと思います。
の近似式を求めてみようと思います。
まず、 の条件式の左辺を
の条件式の左辺を  とおくと、その導関数
とおくと、その導関数  は
は
したがって、 が極値をとるのは
が極値をとるのは  の時です。増減表は
の時です。増減表は
となりますが、 (
( の条件式の右辺値)より、
の条件式の右辺値)より、 の解は 区間
の解は 区間  に1つだけ存在します。
に1つだけ存在します。
そこで、 の特殊値をあげると
の特殊値をあげると
 の時、
の時、 の値が
の値が  と3桁ほど一致しています。そこで、微小量
と3桁ほど一致しています。そこで、微小量  をもって
をもって  とし、
とし、 を
を  で展開して2次で近似しますと
で展開して2次で近似しますと
解くべき式は  の2次方程式となります。
の2次方程式となります。
2次方程式の解の公式から
を得ます。実際に値を計算してみると
と、数値解と8桁目まで一致しました。最後に、ここで求まった  を 運動エネルギーの式に代入して
を 運動エネルギーの式に代入して
を得ます。数値解は  で、やはり8桁目まで一致しています
で、やはり8桁目まで一致しています

単位、そして外力の振幅を
単位,周期を
単位とします。この時、質点の運動方程式は
微分を表します。初め 質点は一点
に固定されていて、時刻
に自由になるとします。すなわち
は
は
に依りません。
は ポンデロモーティブエネルギーと呼ばれます。
のオーダーの運動エネルギー
を得ますが、元の位置
に戻った時の
の取り得る最大の値は
であることが知られています。この
という数字がどの様にして出てきたのか以前から気になっていましたので、今回はこの計算に取り組んでみました
に戻る時刻を
とおくと、
と
で接し,
で交叉する直線の方程式です。下図1のように、
を決めると グラフから
を求めることができます

から
を求める
の場合のみ接線は
に交点を持ち、質点が元の位置に戻ります。
が決まれば、速度は
を最大にするような
の条件式を導くことです。このような条件付き極値問題は、例えばラグランジュの未定乗数法で機械的に解くことができます。未定乗数を
とおけば、ラグランジュ関数は
についての偏微係数をゼロとして条件式を得ます
となり、これを第2式に代入し整理して
と
で接し、
で交叉する直線の方程式です。下図2のように、
が定まると グラフから
を最大にする
の候補
を求めることができます

から
を求める
を決めると
の
での接線を描いて
が求まり、さらに
の
での接線を描いて
が求まります。結局、
となるように
を決めれば良いことになります。この時、グラフは下図3のようになるでしょう

のとき
を中心に
回転させると互いに一致します。ゆえ
の条件式から
を消去して整理しますと
を求めると、
での運動エネルギーの最大値
の条件式は、恐らく
について解析的に解くことができません。そこで、ニュートン・ラフソン法などを使って数値的に解くと
の近似式を求めてみようと思います。
の条件式の左辺を
とおくと、その導関数
は
が極値をとるのは
の時です。増減表は
(
の条件式の右辺値)より、
の解は 区間
に1つだけ存在します。
の特殊値をあげると
の時、
の値が
と3桁ほど一致しています。そこで、微小量
をもって
とし、
を
で展開して2次で近似しますと
の2次方程式となります。
を 運動エネルギーの式に代入して
で、やはり8桁目まで一致しています