Doc's log

ドクログ

ベルトランの定理（Bertrand's theorem）

ベルトランの定理の論文（英訳版）を読み、自分なりに理解したところをまとめました。

Santos, F. C.; Soares, V.; Tort, A. C. (2011). “An English translation of Bertrand's theorem”. Latin American Journal of Physics Education 5 (4): 694–696.


ベルトランの定理

中心力ポテンシャル V(r) に束縛された質点の運動について、質点が必ず安定な閉軌道を描くような V(r) の形は 次の２つに限られます

  1. 万有引力型： V(r)\propto -r^{-1}
  2. 等方調和振動子型： V(r)\propto r^2

証明の準備

２つの保存量

質点の軌道は、ポテンシャル中心を含む１つの平面上におさまります： 質点は この平面に垂直な力を受けないためです。そこで、ラグランジアン \mathcal{L} を 平面極座標 (r,\vartheta) を使って表します。まず、速度 \dot{\mathbf{r}} の表式は

\displaystyle \dot{\mathbf{r}} = \frac{\partial\mathbf{r}}{\partial r}\dot{r} + \frac{\partial\mathbf{r}}{\partial\vartheta}\dot{\vartheta} = \left|\frac{\partial\mathbf{r}}{\partial r}\right|\dot{r}\mathbf{e}_r + \left|\frac{\partial\mathbf{r}}{\partial\vartheta}\right|\dot{\vartheta}\mathbf{e}_\vartheta

なので、そのノルム自乗は 基底 \mathbf{e}_r, \mathbf{e}_\vartheta の直交性から

\displaystyle \dot{\mathbf{r}}^2 = \left|\frac{\partial\mathbf{r}}{\partial r}\right|^2\dot{r}^2 + \left|\frac{\partial\mathbf{r}}{\partial\vartheta}\right|^2\dot{\vartheta}^2

ここで、 \mathbf{r} の極座標表示は

\displaystyle \mathbf{r} = r(\cos\vartheta\mathbf{e}_r+\sin\vartheta\mathbf{e}_\vartheta)

ですから、運動エネルギーは

\displaystyle \frac{M}{2}\dot{\mathbf{r}}^2 = \frac{M}{2}\left(\dot{r}^2 + r^2\dot{\vartheta}^2\right)

となり、ラグランジアン \mathcal{L} の表式は

\displaystyle \mathcal{L} = \frac{M}{2}\left(\dot{r}^2 + r^2\dot{\vartheta}^2\right) - V(r)

  さて、この表式から ２つの保存量が明らかになります。第１に、時刻 t に陽に依存しないことから 全エネルギー

\displaystyle E = \frac{M}{2}\left(\dot{r}^2 + r^2\dot{\vartheta}^2\right) + V(r)

が保存します。第２に、 \vartheta が循環座標となっていることから 角運動量

\displaystyle L = \frac{\partial \mathcal{L}}{\partial\dot{\vartheta}} = Mr^2\dot{\vartheta}

が保存します。

軌道の方程式

ラグランジアンが得られたので オイラー・ラグランジュ方程式を解いても良いですが、いま興味があるのは質点の軌道であって、時間発展を考える意味はありません。 r の \vartheta 依存性、 \mathrm{d}r/\mathrm{d}\vartheta の式が与えられれば十分です。そこで、前項で求めた２つの保存量を \dot{r}, \dot{\vartheta} について解き

\displaystyle \dot{\vartheta} = \frac{L}{Mr^2}\\ \dot{r} = \pm\sqrt{\frac{2}{M}\left(E-V(r)\right)-\frac{L^2}{M^2r^2}}

軌道の方程式（ビネ方程式の変形）

\displaystyle \frac{\mathrm{d}r}{\mathrm{d}\vartheta} = \frac{\dot{r}}{\dot{\vartheta}} = \pm r^2\sqrt{\frac{2M\left(E-V(r)\right)}{L^2}-\frac{1}{r^2}}

を得ます

ポテンシャル中心から 近点と遠点とを見込む角

閉軌道をたどると、中心からの距離が極小となる近点，極大となる遠点が交互に現れます。そこで、隣り合う近点・遠点の１組に注目し、ポテンシャル中心から２点を見込む角を \varphi とおきます。すなわち

\displaystyle \varphi = \int_0^\varphi\mathrm{d}\vartheta = \int_{r_0}^{r_1}\frac{\mathrm{d}r}{\mathrm{d}r/\mathrm{d}\vartheta} = \int_{r_0}^{r_1}{\frac{1}{\sqrt{\frac{2M\left(E-V(r)\right)}{L^2}-\frac{1}{r^2}}}\frac{\mathrm{d}r}{r^2}}

ただし、近点 r=r_0 の方位を \vartheta=0 とし、遠点 r=r_1 の方位を \vartheta=\varphiとしています。 r は 区間 0\lt\vartheta\lt\varphi で単調増加しますから、 \mathrm{d}r/\mathrm{d}\vartheta の復号は + をとります
  積分の \mathrm{d}r/r^2 に注目しますと、 z=1/r と変数変換したくなります。そこで、 \varpi(z) = -V\left(1/z\right) とおくと

\displaystyle \varphi = \int_\alpha^\beta{\frac{\mathrm{d}z}{\sqrt{\frac{2ME}{L^2}+\frac{2M\varpi(z)}{L^2}-z^2}}}

積分区間の \alpha, \beta は、それぞれ 遠点，近点の中心からの距離の逆数 1/r_1, 1/r_0 です。ここで h = 2ME/L^2， 1/k^2=2M/L^2 とおけば 元論文の式 (3) の右辺を得ます

安定な閉軌道とは

『安定な』閉軌道とは、先に求めた軌道の方程式を満たしながら 連続変形させたとき、閉軌道のままであるような軌道です。結論を先に言いますと、閉軌道の条件は「近点と遠点とを見込む角 \varphi が 円周率 \pi の有理数 m 倍であること」，さらに安定である条件は「 m が軌道の連続変形に依らない定数であること」です

閉軌道の条件

中心力を受けて運動する質点の軌道 r=r(\vartheta) は、軌道上に \mathrm{d}r/\mathrm{d}\vartheta=0 となる点（ \vartheta=0 とします）があれば、その点とポテンシャル中心とを結ぶ直線について線対称 r(\vartheta)=r(-\vartheta) になります。それは、軌道の方程式が \vartheta に依存しないことから明らかです。
  さて、閉軌道について考えます。先に考えた 隣り合う近点 (\vartheta=0)・遠点 (\vartheta=\varphi) の組に注目すると、軌道が 遠点とポテンシャル中心とを結ぶ直線について線対称であることから、 \vartheta=2\varphi の点が また近点 (r=r_0) でなければなりません。同様にして、 n を整数として \vartheta=2n\varphi は近点， \vartheta=(2n-1)\varphi は遠点となります。もし \varphi が \pi の有理数倍でなければ、これらの近点・遠点はすべて一致せず、軌道をどれだけ たどっても閉じることはありません。
  したがって、閉軌道の条件は「近点と遠点とを見込む角 \varphi が 円周率 \pi の有理数 m 倍であること (\varphi=m\pi)」です。

安定な閉軌道の条件

軌道を連続変形させれば、 m は連続的に変化するでしょう。ところが、『有理数 m は 無理数を通過しないと別の有理数 m' になれない』ので、安定な閉軌道であるためには m は軌道の連続変形に依らない定数でなければなりません。『』の事実は、例えば２つの有理数 m, m' を 1:\sqrt{2} に内分する数 x を考えれば分かります

\displaystyle x = \frac{m\sqrt{2}+m'}{\sqrt{2}+1} = (2m-m')+\sqrt{2}(m'-m)

右辺の第１項は有理数，第２項は m\neq m' より無理数なので、 x は無理数です。 x は m, m' の間にありますから、 m' をどう選んでも無理数 x を通過することになります
  したがって、安定な閉軌道の条件は「 m が軌道の連続変形に依らない定数であること」です

証明

証明の準備から、安定な閉軌道が満たす方程式は 元論文の式 (3) の通りです。そして、 z=\alpha, \beta で \mathrm{d}r/\mathrm{d}\vartheta=0 となることから、定数 h, 1/k^2 を \alpha, \beta の式で置き換えて 式 (4) を得ます（分母の平方根の最後項の z^3 は恐らく z^2 の誤植です。この記事では z^2 と考えます）
  任意の中心力ポテンシャル V(r)（あるいは \varpi(z)）について、円軌道は 軌道の方程式を満たします。そこで、円軌道を微小変形した軌道が閉軌道である場合を考えます。 \alpha, \beta の差は微小なので、次の u, \gamma は微小量です

\displaystyle u = \beta - \alpha \\ \gamma = z - \alpha

式 (4) の分子・分母を これら２つの微小量で展開し、それぞれ主要項を求めます。分子は 元論文の通り \sqrt{u\varpi'(\alpha)} です。分母は 低次の項がことごとくキャンセルするため、３次まで展開する必要があります。詳しくは次の通りです（簡単のため、引数 \alpha を省略して \varpi(\alpha) を \varpi と表記します）

\displaystyle \begin{aligned} \alpha^2\varpi(\beta) &= \alpha^2\varpi+\alpha^2\varpi'u+\frac{1}{2}\alpha^2\varpi''u^2+\frac{1}{6}\alpha^3\varpi^{(3)}u^3 + \cdots \\ -\beta^2\varpi &= -\alpha^2\varpi-2\alpha\varpi u -\varpi u^2 \\ (\beta^2-\alpha^2)\varpi(z) &= (2\alpha u+u^2)\left(\varpi+\varpi'\gamma+\frac{1}{2}\varpi''\gamma^2+\cdots\right) \\ &= 2\alpha\varpi u + \{2\alpha\varpi'u\gamma+\varpi u^2\} + \{\alpha\varpi''u\gamma^2+\varpi'u^2\gamma\} + \cdots \\ -z^2\{\varpi(\beta)-\varpi\} &= -(\alpha^2+2\alpha\gamma+\gamma^2)\left(\varpi'u+\frac{1}{2}\varpi''u^2+\frac{1}{6}\varpi^{(3)}u^3+\cdots\right) \\ &= -\alpha^2\varpi'u-\left\{\frac{1}{2}\alpha^2\varpi''u^2+2\alpha\varpi'u\gamma\right\}-\left\{\frac{1}{6}\alpha^2\varpi^{(3)}u^3+\alpha\varpi''u^2\gamma+\varpi'u\gamma^2\right\}+\cdots \end{aligned}

上記を足し合わせると ２次以下の項がすべてキャンセルして

\displaystyle \alpha^2\varpi(\beta)-\beta^2\varpi+(\beta^2-\alpha^2)\varpi(z)-z^2\{\varpi(\beta)-\varpi\} \sim u\{\varpi'-\alpha\varpi''\}(u\gamma-\gamma^2)

あとは、これらを式 (4) の分子分母に代入し、 z を \gamma に変数変換して積分を実行します

\displaystyle m\pi = \sqrt{\frac{\varpi'}{\varpi'-\alpha\varpi''}}\int_0^u{\frac{\mathrm{d}\gamma}{\sqrt{u\gamma-\gamma^2}}} = \sqrt{\frac{\varpi'}{\varpi'-\alpha\varpi''}}\pi

すると、元論文にある \varpi の微分方程式が得られます。対数微分の形をしていますから、すぐに解 \varpi が求まります。 \alpha は任意なので z で置き換えて良いでしょう。すなわち

\displaystyle \varpi(z) = A \frac{z^{2-1/m^2}}{2-\frac{1}{m^2}} + B

A, B は積分定数です。ここで求まった \varpi(z) を 再び 式 (4) に代入して 式 (6) を得ます
  最後に 1/m^2-2 の正負で場合分けし、 \alpha, \beta の適当な値を代入すれば、 m の値が１つずつ求まります。 V(r) に戻せば

ベルトランの定理が示されました

疑問点

証明の最後で 理解できていない点が２つあります。

  1. \alpha=0 や \beta=0 を代入している点。 \alpha, \beta は中心からの距離の逆数ですから、その値が 0 になるのは無限遠点 r\uparrow\infty です。これは有界な軌道を考えていることに 矛盾しているように思われます
  2. \alpha=1, \beta=0 を代入している点。 \alpha, \beta は それぞれ中心から遠点，近点までの距離の逆数なので \alpha\lt\beta となる筈であり、矛盾しているように思われます

まだ理解に時間がかかりそうです

終わりに

定理の逆として、万有引力型と等方調和振動子型のポテンシャルのもとで 質点が安定な閉軌道を描くことは 容易に示されます。どちらの場合も 質点は楕円軌道を描き、前者では その焦点の１つが，後者では その中心が ポテンシャル中心となります。それぞれ、導出された m の値と整合しています

回転系の運動方程式

回転系の運動方程式と慣性モーメントを導出します。この記事では、 1\times 1 行列をスカラーと同一視し、ベクトルの内積 \mathbf{a}\cdot\mathbf{b} を \mathbf{a}^T\mathbf{b} と書きます

回転行列

回転の運動は 回転系で記述するのが自然な方法でしょう。しかし、慣性系から回転系に移れば ベクトル量である位置，速度，加速度はそれぞれ変換を受けます。これら 3 次元ベクトルの回転変換は、次の条件を満たす 3\times 3 の回転行列 \mathbf{R} をかけてなされます

\displaystyle \mathbf{R}^T\mathbf{R}= \mathbf{R} \mathbf{R}^T =\mathbf{1}_3

ただし、 \mathbf{1}_3 は 3 次元の単位行列です

※ 行列式をとれば \det \mathbf{R} =\pm 1 となりますが、この記事では 反転を含む変換 \det\mathbf{R}=-1 は考えません

説明
回転変換は、任意のベクトル \mathbf{a}, \mathbf{b} の大きさとその間の角度を変えないため、内積を変えない変換です。そこで、回転変換後のベクトルを \mathbf{a}'=\mathbf{R}\mathbf{a}, \mathbf{b}'=\mathbf{R}\mathbf{b} とおいて内積をとれば

\displaystyle \mathbf{a}'^T\mathbf{b}'=(\mathbf{R}\mathbf{a})^T(\mathbf{R}\mathbf{b})=\mathbf{a}^T\mathbf{R}^T\mathbf{R}\mathbf{b}=\mathbf{a}^T\mathbf{b}

となります。これが任意の \mathbf{a}, \mathbf{b} について成り立つので \mathbf{R}^T\mathbf{R}=\mathbf{1}_3 を得ます。また、これに左から \mathbf{R}，右から \mathbf{R}^{-1} をかければ \mathbf{R}\mathbf{R}^T=\mathbf{1}_3 を得ます
  なお、正確には 内積を変えない変換には反転も含まれ、回転と合わせて直交変換と呼ばれます。行列式は \det\mathbf{R}=\pm 1 ですが、反転を含まない回転変換が \det\mathbf{R}=+1 です。それは、任意の回転は 恒等変換（無回転）からの無限小回転の連続で与えられ、行列式の値が +1 から -1 に飛び越えようがないためです

速度の回転変換

慣性系における位置ベクトルを \boldsymbol{x}_I，これを回転系に移したものを \boldsymbol{x}_R と置きます。適当な直交行列 \mathbf{R} をもって

\displaystyle \boldsymbol{x}_I = \mathbf{R} \boldsymbol{x}_R

と表せます。両辺を時間で微分すれば

\displaystyle \dot{\boldsymbol{x}}_I = \mathbf{R} \dot{\boldsymbol{x}}_R + \dot{\mathbf{R}} \boldsymbol{x}_R

ここで \dot{\mathbf{R}} が初登場しましたので、自然な発想として 直交行列の性質 \mathbf{R}^T \mathbf{R}=\mathbf{1}_3 の時間微分を調べてみる気になります。すると

\displaystyle \dot{\mathbf{R}}^T\mathbf{R}+\mathbf{R}^T\dot{\mathbf{R}}=0

より

\displaystyle \dot{\mathbf{R}}^T\mathbf{R} = (\mathbf{R}^T\dot{\mathbf{R}})^T = -\mathbf{R}^T\dot{\mathbf{R}}

を得ます。そこで \mathbf{\Omega}=\mathbf{R}^T\dot{\mathbf{R}} と置くと、これは歪対称行列になっています

\displaystyle \mathbf{\Omega}^T=-\mathbf{\Omega}

\dot{\boldsymbol{x}}_I の表式の両辺に \mathbf{R}^T をかけて \dot{\mathbf{R}} を消去すれば

\displaystyle \mathbf{R}^T\dot{\boldsymbol{x}}_I=\dot{\boldsymbol{x}}_R + \mathbf{\Omega} \boldsymbol{x}_R

慣性系における速度 \dot{\boldsymbol{x}}_I は、回転系での見かけの速度 \dot{\boldsymbol{x}}_R と 座標の回転に由来する速度 \mathbf{\Omega} \boldsymbol{x}_R の和に変換されます

\mathbf{\Omega} について補足

\mathbf{\Omega} は角速度を表す行列です。このことは \mathbf{\Omega} の成分を考えると分かりやすいでしょう。先ず 歪対称行列 \mathbf{\Omega} は適当な実数 a, b, c をもって

\displaystyle \mathbf{\Omega}= \begin{pmatrix} 0&-a&-b\\ a&0&-c\\ b&c&0 \end{pmatrix}

と表されます。これを \boldsymbol{x}_I にかければ

\displaystyle \mathbf{\Omega}\boldsymbol{x}_I= \begin{pmatrix} 0&-a&-b\\ a&0&-c\\ b&c&0 \end{pmatrix} \begin{pmatrix} x\\ y\\ z \end{pmatrix} = \begin{pmatrix} -ay-bz\\ -cz+ax\\ bx+cy \end{pmatrix}

となり、結果はベクトルの外積のような形をしています。事実、 a=\omega_z, b=-\omega_y, c=\omega_x とおけば

\displaystyle \mathbf{\Omega}\boldsymbol{x}_I= \begin{pmatrix} 0&-\omega_z&\omega_y\\ \omega_z&0&-\omega_x\\ -\omega_y&\omega_x&0 \end{pmatrix} \begin{pmatrix} x\\ y\\ z \end{pmatrix} = \begin{pmatrix} \omega_y z-\omega_z y\\ \omega_z x-\omega_x z\\ \omega_x y-\omega_y x \end{pmatrix} = \begin{pmatrix} \omega_x\\ \omega_y\\ \omega_z \end{pmatrix} \times \begin{pmatrix} x\\ y\\ z \end{pmatrix} = \boldsymbol{\omega}\times\boldsymbol{x}_I

このように 歪対称行列は ベクトルの外積の形で書かれます：こういったベクトルを特に軸性ベクトルと呼びます。 \boldsymbol{\omega} は 位置ベクトル \boldsymbol{x}_I と外積をとって速度となりますから、これは角速度ベクトルそのものです。
  次に、外積を使わずに考えてみます。先ず \mathbf{\Omega} を次のように分けます

\displaystyle \mathbf{\Omega}= \begin{pmatrix} 0&-\omega_z&\omega_y\\ \omega_z&0&-\omega_x\\ -\omega_y&\omega_x&0 \end{pmatrix} = \begin{pmatrix} 0&0&0\\ 0&0&-1\\ 0&1&0 \end{pmatrix} \omega_x+ \begin{pmatrix} 0&0&1\\ 0&0&0\\ -1&0&0 \end{pmatrix} \omega_y+ \begin{pmatrix} 0&-1&0\\ 1&0&0\\ 0&0&0 \end{pmatrix} \omega_z=\mathbf{\Omega}_x+\mathbf{\Omega}_y+\mathbf{\Omega}_z

\mathbf{\Omega} の定義より \dot{\mathbf{R}}=\mathbf{R}\mathbf{\Omega} ですから、時刻 t+\Delta t における回転行列 \mathbf{R}(t+\Delta t) は 微小時間 \Delta t の一次近似で

\displaystyle \begin{aligned} \mathbf{R}(t+\Delta t)&\sim\mathbf{R}(t)+\dot{\mathbf{R}}(t)\Delta t=\mathbf{R}(t)(\mathbf{1}_3+\mathbf{\Omega}\Delta t)\\ &\sim\mathbf{R}(t)(\mathbf{1}_3+\mathbf{\Omega}_x\Delta t)(\mathbf{1}_3+\mathbf{\Omega}_y\Delta t)(\mathbf{1}_3+\mathbf{\Omega}_z\Delta t) \end{aligned}

となります。そこで \Delta t での x 軸まわりの回転角（右ねじの向きを正とします）を \Delta\theta_x\sim\omega_x\Delta t などと書けば

\displaystyle \mathbf{1}_3+\mathbf{\Omega}_x\Delta t\sim \begin{pmatrix} 1&0&0\\ 0&1&-\Delta\theta_x\\ 0&\Delta\theta_x&1 \end{pmatrix} \sim \begin{pmatrix} 1&0&0\\ 0&\cos\Delta\theta_x&-\sin\Delta\theta_x\\ 0&\sin\Delta\theta_x&\cos\Delta\theta_x \end{pmatrix}
\displaystyle \mathbf{1}_3+\mathbf{\Omega}_y\Delta t\sim \begin{pmatrix} 1&0&\Delta\theta_y\\ 0&1&0\\ -\Delta\theta_y&0&1 \end{pmatrix} \sim \begin{pmatrix} \cos\Delta\theta_y&0&\sin\Delta\theta_y\\ 0&1&0\\ -\sin\Delta\theta_y&0&\cos\Delta\theta_y \end{pmatrix}
\displaystyle \mathbf{1}_3+\mathbf{\Omega}_z\Delta t\sim \begin{pmatrix} 1&-\Delta\theta_z&0\\ \Delta\theta_z&1&0\\ 0&0&1 \end{pmatrix} \sim \begin{pmatrix} \cos\Delta\theta_z&-\sin\Delta\theta_z&0\\ \sin\Delta\theta_z&\cos\Delta\theta_z&0\\ 0&0&1 \end{pmatrix}

それぞれ x, y, z 軸まわりの微小回転（右ねじ）を表していることが分かります。ゆえ \mathbf{\Omega}\Delta t は 任意の微小回転を表し、 \mathbf{\Omega} は \Delta t\to 0 の極限で角速度を表します

回転系の運動方程式

加速度の表式を得るため、先に得た 速度の回転変換の式をさらに時間微分します

\displaystyle \mathbf{R}^T\ddot{\boldsymbol{x}}_I+\dot{\mathbf{R}}^T\dot{\boldsymbol{x}}_I=\ddot{\boldsymbol{x}}_R +\mathbf{\Omega} \dot{\boldsymbol{x}}_R+\dot{\mathbf{\Omega}} \boldsymbol{x}_R

左辺第２項の速度 \dot{\boldsymbol{x}}_I の項が邪魔ですから、再び速度の回転変換の式を使って これを消去します

\displaystyle \dot{\mathbf{R}}^T\dot{\boldsymbol{x}}_I = \dot{\mathbf{R}}^T (\mathbf{R} \mathbf{R}^T) \dot{\boldsymbol{x}}_I = (\mathbf{R}^T\dot{\mathbf{R}})^T \mathbf{R}^T\dot{\boldsymbol{x}}_I = -\mathbf{\Omega}(\dot{\boldsymbol{x}}_R+\mathbf{\Omega}\boldsymbol{x}_R)

もとの式に戻して整理すれば、加速度の回転変換の表式を得ます

\displaystyle \mathbf{R}^T\ddot{\boldsymbol{x}}_I=\ddot{\boldsymbol{x}}_R+\mathbf{\Omega}^2\boldsymbol{x}_R+2\mathbf{\Omega}\dot{\boldsymbol{x}}_R+\dot{\mathbf{\Omega}}\boldsymbol{x}_R

回転系での加速度の項 \ddot{\boldsymbol{x}}_R について解き、質量 m をかければ回転系の運動方程式を得ます

\displaystyle m\ddot{\boldsymbol{x}}_R=\mathbf{R}^T m\ddot{\boldsymbol{x}}_I-m\mathbf{\Omega}^2\boldsymbol{x}_R-2m\mathbf{\Omega}\dot{\boldsymbol{x}}_R-m\dot{\mathbf{\Omega}}\boldsymbol{x}_R

右辺第１項は、質点に作用する力を回転系で見たものです。第２項からは全て見かけの力で、それぞれ順に遠心力，コリオリ力、オイラー力と呼ばれます。この内、遠心力は回転系で必ず現れる力です。他方、コリオリ力は 質点が回転系で静止する場合 \dot{\boldsymbol{x}}_R= 0 ，オイラー力は 等角速度系の場合 \dot{\mathbf{\Omega}}=0 には現れない力です
  ベクトル表記するには、 \mathbf{\Omega} を \boldsymbol{\omega}\times で置き換えます。ついでに 質点に作用する力を回転系で見たものを \mathbf{F}_R とおいて

\displaystyle m\ddot{\boldsymbol{x}}_R=\mathbf{F}_R-m\boldsymbol{\omega}\times(\boldsymbol{\omega}\times\boldsymbol{x}_R)-2m\boldsymbol{\omega}\times\dot{\boldsymbol{x}}_R-m\dot{\boldsymbol{\omega}}\times\boldsymbol{x}_R

慣性モーメント

運動量 \mathbf{p} は 慣性質量 m と速度 \dot{\boldsymbol{x}} の積で定義されます。これに倣い、角運動量 \mathbf{L} = \boldsymbol{x}\times\mathbf{p} を 慣性モーメント \mathbf{I} と角速度 \boldsymbol{\omega} の積の形で表します。まず、 \mathbf{L} の式をできるところまで変形します

\displaystyle \mathbf{L} = \boldsymbol{x}\times\mathbf{p} = \boldsymbol{x}\times m\dot{\boldsymbol{x}} = m\boldsymbol{x}\times(\boldsymbol{\omega}\times\boldsymbol{x}) = -m\boldsymbol{x}\times(\boldsymbol{x}\times\boldsymbol{\omega})

先ほど確認したように、ベクトルの外積（ここでは \boldsymbol{x}\times）は 歪対称行列 \mathbf{X} で表されます。その成分は \mathbf{\Omega} の成分と同様に考えて

\displaystyle \mathbf{X}=\begin{pmatrix} 0&-z&y\\ z&0&-x\\ -y&x&0 \end{pmatrix}

ですから、慣性モーメント \mathbf{I} は

\displaystyle \mathbf{I}=-m\mathbf{X}^2 = -m\begin{pmatrix} -(y^2+z^2)&xy&zx\\ xy&-(z^2+x^2)&yz\\ zx&yz&-(x^2+y^2) \end{pmatrix} = m\left(\boldsymbol{x}^T\boldsymbol{x}\mathbf{1}_3-\boldsymbol{x}\boldsymbol{x}^T\right)

となります。
 なお、同じことですが、歪対称行列 \mathbf{X} を経ずに ベクトル三重積 \boldsymbol{x}\times(\boldsymbol{x}\times\boldsymbol{\omega}) を直接計算して導くこともできます。アインシュタインの縮約記法を使えば、三重積の j (\in \{x,y,z\}) 成分 は

\displaystyle \epsilon_j{}^{kl}x_k\epsilon_l{}^{mn}x_m\omega_n = (\epsilon^l{}_j{}^k\epsilon_l{}^{mn})x_k x_m\omega_n= (\delta_j^m\delta^{kn}-\delta_j^n\delta^{km})x_k x_m\omega_n = x_k x_j \omega^k - x_k x^k \omega_j

ただし、 \epsilon_j{}^{kl} 等はレヴィ＝チヴィタのイプシロン、 \delta_j^m 等はクロネッカーのデルタです。途中式の () の中で縮約公式を用いています。右辺は x_j \boldsymbol{x}^T\boldsymbol{\omega} - \boldsymbol{x}^T\boldsymbol{x}\omega_j と書けますので、結局ベクトル三重積は

\displaystyle \boldsymbol{x}\times(\boldsymbol{x}\times\boldsymbol{\omega}) = \boldsymbol{x} \boldsymbol{x}^T\boldsymbol{\omega} - \boldsymbol{x}^T\boldsymbol{x}\boldsymbol{\omega}=-(\boldsymbol{x}^T\boldsymbol{x}\mathbf{1}_3-\boldsymbol{x} \boldsymbol{x}^T)\boldsymbol{\omega}

-m を乗じて \mathbf{I}\boldsymbol{\omega} を得ます
  さて、外力 \mathbf{F} は 運動量 \mathbf{p} を時間変化させます

\displaystyle \dot{\mathbf{p}}=m\dot{\mathbf{v}}=\mathbf{F}

では、角運動量は 何によって時間変化するのでしょうか。角運動量を時間微分すれば

\displaystyle \dot{\mathbf{L}}=\frac{\mathrm{d}}{\mathrm{d}t}(\mathbf{r}\times\mathbf{p}) = \dot{\mathbf{r}}\times m\dot{\mathbf{r}} + \mathbf{r}\times m\ddot{\mathbf{r}} = \mathbf{r}\times\mathbf{F} = \mathbf{N}

右辺に現れた 位置ベクトルと外力の外積 \mathbf{N} は トルクと呼ばれます。すなわち、角運動量はトルク \mathbf{N} により時間変化します。特に、慣性モーメント \mathbf{I} が時間変化しないような座標をとれば

\displaystyle \dot{\mathbf{L}}= \mathbf{I}\dot{\boldsymbol{\omega}} = \mathbf{N}

となり、並進の運動方程式と対称的な形式が導かれます

高校物理再考　力学１

物理の知識を整理するため、まず高校物理の力学の内容を振り返ってみました。このページの目的は飽くまで自分の理解／無理解を明確にすることですから、ここでは持って回った表現を避け、あえて「〇〇とは△△のことだ」などと断言する形を採っています。「誤りと分かった時点で修正すれば良い」というスタンスですので、まかり間違えて（？）この過疎ログを訪れてしまった方は、以下の内容をどうか信用なさらないようお願いします

物理学とは

かつて物理学者ガリレオ・ガリレイは、「自然という書物は数学の言葉で書かれている」と言いました。このガリレイのテーゼを是とすれば、自然界のあまねく現象は「数学界」において完璧に再現され、そこでは計算によって全てを知れることになります。物理学とは、数学を介して自然現象の本質を理解しようとする試みの総称です
  物理学の諸理論は「自然現象を描写する数学はこういうものだ」という解釈（指導原理と言います）を与えた後、数学により構築されます。指導原理の与え方は自由ですが 自然現象の本質を突く物理学の理論は次の要件を満たさねばなりません

  • 指導原理が簡潔である
  • 広範な自然現象の観測事実を正確に描写する

こうした理論に 力学、熱力学、電磁気学、・・・等々があり、高校物理ではその基礎を学びます

力学とは

力学は 物理学者アイザック・ニュートンが創始した理論体系です。ニュートンの運動３法則（＆万有引力の法則）を指導原理とし、質量を持つ一般の物体（ボール、車、惑星、・・・等々）の運動を統一的に描写します。ここでは先ず理論の背景知識をまとめ、最後にニュートンの運動３法則に触れます

絶対時間・絶対空間

ニュートンは、時間の流れと空間の広がりは全宇宙で一様であり、また互いに独立して存在すると考えました：これを絶対時間・絶対空間と呼びます。そして「物体の運動」とは「物体の位置が 絶対時間の経過とともに絶対空間の中を移動すること」であると捉え、物体の運動が満たすべき法則を定式化しました

観測者

物体の運動を数式で記述するためには、まず物体の位置を指定するための座標系を置かねばなりません。この座標系を 特に観測者と呼びます。観測 ”者” という言葉から 物体の運動を観測する ”人間” をイメージしても良いですが、その場合、観測者は究極のジコチューであることに気を付ける必要があります。例えば、歩いている観測者ならば「自身は静止していて世界が後ろに動いている」と考えますし、回転している観測者ならば「自身は静止していて世界が逆に回転している」と考えます。つまり、観測者は常に 自身が絶対的に静止していると考えます。それゆえ、いち物体の運動を記述するために 同時に複数の観測者を考えることは通常ありません。観測同士がカチ合うからです

慣性の法則

物体に作用する力の合計（合力）がゼロのとき、物体が静止ないしは等速直線運動（まとめて慣性運動と呼びます）を続けるならば、慣性の法則が成り立っていると言います。慣性の法則は、観測者の選び方によっては 必ずしも成り立ちません。そこで、慣性の法則が成り立つように選んだ座標系のことを 特に慣性系と呼びます

加速度運動

慣性運動以外の運動を、加速度運動と呼びます。加速度運動では、速度が時々刻々と変化するため「きはじの法則」を使うことができません。そこで、速度を位置 \vec{r} の時間微分として再定義します

\displaystyle \dot{\vec{r}}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}

この様に「時間微分を上付きドットで表す方法」を、ニュートン記法と呼びます
さらに、加速の度合いを表す量として加速度

\displaystyle \ddot{\vec{r}}=\frac{\mathrm{d}\dot{\vec{r}}}{\mathrm{d}t}

を導入します。加速度 \ddot{\vec{r}} を時間積分すると速度 \dot{\vec{r}}、さらに時間積分すると位置 \vec{r} が求まります。不定積分を行う度に積分定数がつきますが、速度につく積分定数を初期速度（初速）、位置につく積分定数を初期位置と呼びます

ニュートンの運動３法則

質量を持つ一般の物体の運動は、次の法則に従います。

  • 第１法則： 慣性系の存在

  • 第２法則： 運動方程式

    • 慣性系において、物体は受けた力 \vec{F} に比例する加速度 \ddot{\vec{r}} を得る
    \displaystyle m\ddot{\vec{r}} = \vec{F}
    • 比例係数 m は物体に固有の量であり、これを（慣性）質量と呼ぶ。質量が大きいほど加速されにくい

  • 第３法則： 作用・反作用の法則

    • 慣性系において、２つの物体が接触して互いに力を及ぼす時、一方の力は他方の力と同じ大きさで、逆を向き、同一直線上にある

力学の問題を解く

力学の問題を解くとは、物体の位置 \vec{r} と速度 \dot{\vec{r}} を時刻 t の関数として求めることです。ここでは幾つかの例題を解きます。基本的な流れは次の通りです：

  1. 慣性系と時刻 t=0 とを定める（どう定めても良い）
  2. 運動方程式を立てる
  3. 運動方程式を解いて 位置 \vec{r}(t) および 速度 \dot{\vec{r}}(t) を得る

以下、重力加速度を g と表記します。また、特に断らない限り空気抵抗や摩擦は考えないものとします

自由落下

  • 問： 質量 m の小球を空中で静かに放したとき、その後の小球の運動を求めよ

  • 答：

    1. 小球の運動は直線的だから、座標は１次元で十分（ \vec{r}=x）。そこで、小球を放す位置を x=0、時刻を t=0 とし、鉛直下向きに x 軸を定める

      自由落下

    2. 小球に作用する力は鉛直下向き（ x 軸正方向）の重力 mg のみだから、運動方程式は

      \displaystyle m\ddot{x} = mg

      すなわち \ddot{x} = g である

    3. 一度積分して速度

      \displaystyle \dot{x}(t) = gt + v_0
      を得る。ここで v_0 は初速（積分定数）だが、問題の条件「静かに放す」より \dot{x}(0)=v_0=0 である。よって

      \displaystyle \dot{x}(t) = gt

      次に、再度積分して位置

      \displaystyle x(t) = \frac{1}{2}gt^2 + x_0

      を得る。ここで x_0 は初期位置（積分定数）だが、1. で自分でおいた座標の設定から x(0) = x_0 = 0 である。よって

      \displaystyle x(t) = \frac{1}{2}gt^2

斜面の降下

  • 問： 質量 m の小球を傾斜角 \theta の斜面に静置した時、その後の小球の運動を求めよ

  • 答：

    1. 小球の運動は直線的だから、座標は１次元で十分（ \vec{r}=x）。そこで、小球を静置する位置を x=0、時刻を t=0 とし、斜面に沿って下向きに x 軸を定める

      斜面の降下

    2. 小球に作用する力は重力 mg のみ（正確には斜面から抗力も受けるが、 x 軸方向の運動には関係ない）で、その x 軸方向成分は mg\sin\theta である。よって、運動方程式は

      \displaystyle m\ddot{x} = mg\sin\theta

      すなわち \ddot{x} = g\sin\theta である

    3. 一度積分して速度

      \displaystyle \dot{x}(t) = (g\sin\theta)t + v_0
      を得る。ここで v_0 は初速だが、問題の条件「静置する」より \dot{x}(0)=v_0=0 である。よって

      \displaystyle \dot{x}(t) = (g\sin\theta)t

      次に、再度積分して位置

      \displaystyle x(t) = \frac{1}{2}(g\sin\theta)t^2 + x_0

      を得る。ここで x_0 は初期位置だが、座標の設定から x(0) = x_0 = 0 である。よって

      \displaystyle x(t) = \frac{1}{2}(g\sin\theta)t^2

  • 念のため、極端な場合を考えてみる

    • \theta = 0 deg の時、斜面は水平面になる。この時、 x(t) = 0、つまり小球は初期位置に静止する。これは直観にあっている

    • \theta = 90 deg の時、斜面は絶壁（鉛直）になる。この時

      \displaystyle x(t) = \frac{1}{2} gt^2
      これは先の自由落下の結果と一致し、整合性がとれている

斜方投げ上げ

  • 問： 質量 m の小球を仰角 \theta、初速 v_0 で投げ上げた時、その後の小球の運動を求めよ

  • 答：

    1. 小球の運動は平面的だから、座標は２次元で十分（ \vec{r}=(x,y)）。そこで、小球を投げ上げる位置を (0, 0)、時刻を t=0 とし、水平方向に x 軸、鉛直上向きに y 軸を定める

      斜方投げ上げ

    2. 小球に作用する力は鉛直下向き（ y 軸負方向）の重力 m\vec{g}=(0, -mg) のみだから、運動方程式は

      \displaystyle m\ddot{\vec{r}} = m\vec{g}
      すなわち \ddot{\vec{r}} = \vec{g} である。成分ごとに分けて書けば

      \displaystyle \ddot{x} = 0\\ \ddot{y} = -g

    3. 成分ごとに分けて解く。なお、初速の x 成分は v_0\cos\theta、 y 成分は v_0\sin\theta であることに注意する

      • x 成分：
        一度積分して速度

        \displaystyle \dot{x}(t) = v_0\cos\theta

        を得る。また、再度積分して位置

        \displaystyle x(t) = (v_0\cos\theta)t + x_0

        を得る。ここで x_0 は初期位置だが、座標の設定から x(0) = x_0 = 0 である。よって

        \displaystyle x(t) = (v_0\cos\theta)t

      • y 成分：
        一度積分して速度

        \displaystyle \dot{y}(t) = -gt + v_0\sin\theta

        を得る。また、再度積分して位置

        \displaystyle y(t) = -\frac{1}{2}gt^2 + (v_0\sin\theta)t + y_0

        を得る。ここで y_0 は初期位置だが、座標の設定から y(0) = y_0 = 0 である。よって

        \displaystyle y(t) = -\frac{1}{2}gt^2 + (v_0\sin\theta)t

  • ついでに、 x と y の関係式を求める。3. で得られた結果から媒介変数 t を消去することで得られ、これを軌跡と呼ぶ。 x(t) の式を t について解いたものを y(t) の式に代入すれば

    \displaystyle \begin{align} y &= -\frac{1}{2}g(x/v_0\cos\theta)^2 + (v_0\sin\theta)(x/v_0\cos\theta) \\ &= -\frac{g}{2(v_0\cos\theta)^2}\left(x-\frac{v_0^2\sin\theta\cos\theta}{g}\right)^2 + \frac{(v_0\sin\theta)^2}{2g} \end{align}

    これは、頂点 (v_0^2\sin\theta\cos\theta / g, (v_0\sin\theta)^2 / (2g)) で、上に凸の放物線である

単振動

  • 問： ばね定数 k のばねに質量 m の小球を吊るす。小球を引っ張り、つり合いの位置から A だけずれた所で静かに放した時、この後の小球の運動を求めよ

  • 答：

    1. 小球の運動は直線的だから、座標は１次元で十分（ \vec{r}=x）。そこで、ばねの自然長の先を x=0、小球を放す時刻を t=0 とし、鉛直下向きに x 軸を定める

      単振動

    2. 小球に作用する力は鉛直下向き（ x 軸正方向）の重力 mg と、ばねの復元力 -kx のみだから、運動方程式は

      \displaystyle \begin{align} m\ddot{x} &= mg - kx \\ \ddot{x} &= -\frac{k}{m}\left(x-\frac{mg}{k}\right) \end{align}

      つり合いの位置は x=mg/k である

    3. この微分方程式を解けば良いが、右辺に x(t) が含まれていて、今までの様に両辺をそのまま積分することができない。そこで

      \displaystyle \frac{\mathrm{d}^2}{\mathrm{d}t^2}\left(x-\frac{mg}{k}\right) = -\frac{k}{m}\left(x-\frac{mg}{k}\right)

      と変形（ mg/k は定数で、微分するとゼロになることに注意）し、つり合いの位置からの変位を x'(t) = x(t)-mg/k と置くと

      \displaystyle \ddot{x}'(t) = -\frac{k}{m}x'(t)

      となり、「２度微分を行うと、元の関数を負の定数倍した関数になる」ことを表す微分方程式に還元される。ここで、高校数学 III の微分の知識で説明できる次の事実を用いる

      関数 f=f(s) が微分方程式

      \displaystyle \frac{\mathrm{d}^2}{\mathrm{d}s^2}f(s) = -a^2f(s)

      を満たす（ a は正の定数）時、その解は次の形を持つ

      \displaystyle f(s) = c\cos(as+\phi)

      また、その微分は

      \displaystyle \frac{\mathrm{d}}{\mathrm{d}s}f(s) = -ac\sin(as+\phi)

      ただし、 c, \phi はそれぞれ積分定数で、 c は正の実数、 \phi は -\pi\lt\phi\le+\pi の実数とする

      上の式で a=\sqrt{k/m} とすれば、解は

      \displaystyle \begin{align} x'(t) &= c\cos\left(\sqrt{\frac{k}{m}}t+\phi\right) \\ \dot{x}'(t) &= -\sqrt{\frac{k}{m}}c\sin\left(\sqrt{\frac{k}{m}}t+\phi\right) \end{align}

      と表される。あとは、問題条件より x'(0) = c\cos\phi = A かつ \dot{x}'(0)=-\sqrt{k/m}c\sin\phi=0 が満たされれば良い。先ず、後者の式で c は非ゼロの定数だから \phi=0 であり、ゆえに前者の式は c=A となる。結局、 x(t) = x'(t)+mg/k とその微分 \dot{x}(t) = \dot{x}'(t) は

      \displaystyle \begin{align} x(t) &= A\cos\left(\sqrt{\frac{k}{m}}t\right) + \frac{mg}{k} \\ \dot{x}(t) &= -\sqrt{\frac{k}{m}}A\sin\left(\sqrt{\frac{k}{m}}t\right) \end{align}

      である

空気抵抗のある落下

  • 問： 質量 m の小球を空中で静かに放したとき、その後の小球の運動を求めよ。
    ただし、小球はその速度に比例する空気抵抗（粘性抵抗）を受ける。比例係数を \kappa とする

  • 答：

    1. 小球の運動は直線的だから、座標は１次元で十分（ \vec{r}=x）。そこで、小球を放す位置を x=0、時刻を t=0 とし、鉛直下向きに x 軸を定める

      空気抵抗のある落下

    2. 小球に作用する力は鉛直下向き（ x 軸正方向）の重力 mg と、速度と反対向きの空気抵抗 -\kappa \dot{x} の２つのみである。よって運動方程式は

      \displaystyle \begin{align} m\ddot{x} &= mg - \kappa \dot{x} \\ \ddot{x} &= -\frac{\kappa}{m} (\dot{x}-\frac{mg}{\kappa}) \end{align}

      \dot{x}(t) = mg/\kappa の時、 \ddot{x}=0 となり加速が止まる。この速度を終端速度と呼ぶ。

    3. この微分方程式を解けば良いが、右辺に \dot{x}(t) が含まれていて、両辺をそのまま積分することができない。そこで

      \displaystyle \frac{\mathrm{d}}{\mathrm{d}t}\left(\dot{x}-\frac{mg}{\kappa}\right) = -\frac{\kappa}{m}\left(\dot{x}-\frac{mg}{\kappa}\right)

      と変形（ mg/\kappa は定数で、微分するとゼロになることに注意）し、 \dot{x}'(t) = \dot{x}(t)-mg/\kappa と置くと

      \displaystyle \frac{\mathrm{d}}{\mathrm{d}t}\dot{x}'(t) = -\frac{\kappa}{m}\dot{x}'(t)

      となり、「１度微分を行うと、元の関数を定数倍した関数になる」ことを表す微分方程式に還元される。ここで、高校数学 III の微分の知識で説明できる次の事実を用いる

      関数 f=f(s) が微分方程式

      \displaystyle \frac{\mathrm{d}}{\mathrm{d}s}f(s) = af(s)

      を満たす（ a は定数）時、その解は次の形を持つ

      \displaystyle f(s) = c\exp(as)

      また、その積分は

      \displaystyle \int f(s) \mathrm{d}s = \frac{1}{a}c\exp(as) + d

      ただし、 c, d は積分定数である

      上の式で a=-\kappa/m とすれば、解は

      \displaystyle \begin{align} \dot{x}'(t) &= c\exp\left(-\frac{\kappa}{m}t\right) \\ x'(t) &= \int \dot{x}'(t) \mathrm{d}t = -\frac{m}{\kappa}c\exp\left(-\frac{\kappa}{m}t\right) + d \end{align}

      と表される。 \dot{x}(t) = \dot{x}'(t)+mg/\kappa とその積分 x(t) = x'(t) + (mg/\kappa)t に直せば

      \displaystyle \begin{align} \dot{x}(t) &= c\exp\left(-\frac{\kappa}{m}t\right)+\frac{mg}{\kappa} \\ x(t) &= -\frac{m}{\kappa}c\exp\left(-\frac{\kappa}{m}t\right) + \frac{mg}{\kappa}t + d \end{align}

      あとは、問題条件より

      \displaystyle \begin{align} \dot{x}(0) &= c + \frac{mg}{\kappa} = 0 \\ x(0) &= -\frac{m}{\kappa}c +d = 0 \end{align}

      が満たされれば良い。先ず、前者の式で c=- mg/\kappa であり、ゆえに後者の式から d=-(m/\kappa)^2g となる。結局

      \displaystyle \begin{align} x(t) &= \frac{mg}{\kappa}\left[t+\frac{m}{\kappa}\exp\left(-\frac{\kappa}{m}t\right)\right] -\left(\frac{m}{\kappa}\right)^2g \\ \dot{x}(t) &= \frac{mg}{\kappa}\left[1-\exp\left(-\frac{\kappa}{m}t\right)\right] \end{align}

      である

振動する外場に揺さぶられる質点の運動 (quiver motion)

問題

単振動する一様な外場に揺すぶられる質点の運動を考えます。質点の質量を 1 単位、そして外力の振幅を 1 単位，周期を 2\pi 単位とします。この時、質点の運動方程式は

\displaystyle \ddot{x}(t) = \cos t

となります：上付きドットは時間 t 微分を表します。初め 質点は一点に固定されていて、時刻 t=t_0 に自由になるとします。すなわち

\displaystyle \dot{x}(t=t_0) = 0 \\ x(t=t_0) = 0

ゆえ運動方程式を時間積分して

\displaystyle \dot{x}(t) = \sin t-\sin t_0 \\ x(t) = -\cos t -t\cos t_0 +(\cos t_0 +t_0\sin t_0)

を得ます。ここで、運動エネルギー K は

\displaystyle K=\frac{\dot{x}^2}{2}=\frac{1}{2}\sin^2t_0-\sin t_0\sin t+\frac{1}{2}\sin^2t

ですが、このうち時間変化する項の時間平均 U_p は

\displaystyle \begin{aligned} U_p &= \int_0^{2\pi} \mathrm{d}t \; \left(K-\frac{1}{2}\sin^2t_0\right) \\ &=\int_0^{2\pi} \mathrm{d}t\; \left(-\sin t_0\sin t+\frac{1}{2}\sin^2t\right) \\ &=0+\frac{1}{4} \end{aligned}

となり、時刻 t_0 に依りません。 U_p=1/4 は ポンデロモーティブエネルギーと呼ばれます。
  さて、質点は外場に揺さぶられて U_p のオーダーの運動エネルギー K を得ますが、元の位置 x=0 に戻った時の K の取り得る最大の値は \sim 3.17U_p であることが知られています。この 3.17 という数字がどの様にして出てきたのか以前から気になっていましたので、今回はこの計算に取り組んでみました

解くべき式

質点が元の位置 x=0 に戻る時刻を t=t_1 とおくと、

\displaystyle \begin{aligned} x(t_1)=-\cos t_1-t_1\sin t_0+(\cos t_0+t_0\sin t_0)=0 \end{aligned}

より

\displaystyle \begin{aligned} -\sin t_0=\frac{\cos t_1-\cos t_0}{t_1-t_0} \end{aligned}

この式は、 \cos t と t=t_0 で接し， t=t_1 で交叉する直線の方程式です。下図１のように、 t=t_0 を決めると グラフから t=t_1 を求めることができます

図１　 t=t_0 から t=t_1 を求める

図から分かる通り、 0\lt t_0\lt 0.5\pi の場合のみ接線は t\gt t_0 に交点を持ち、質点が元の位置に戻ります。
  さて、 t=t_1 が決まれば、速度は

\displaystyle \begin{aligned} \dot{x}(t_1)=\sin t_1-\sin t_0 \end{aligned}

と与えられます。そこで、当面の目標は 速さ |\sin t_1-\sin t_0| を最大にするような t_0, t_1 の条件式を導くことです。このような条件付き極値問題は、例えばラグランジュの未定乗数法で機械的に解くことができます。未定乗数を \lambda とおけば、ラグランジュ関数は

\displaystyle \begin{aligned} \mathcal{L}(t_0, t_1, \lambda)=\sin t_1-\sin t_0 +\lambda\left(-\cos t_1-t_1\sin t_0+(\cos t_0+t_0\cos t_0)\right) \end{aligned}

と書けます。そこで、 t_0, t_1 についての偏微係数をゼロとして条件式を得ます

\displaystyle \begin{aligned} \frac{\partial\mathcal{L}}{\partial t_0} &= -\left\{1+\lambda(t_1-t_0)\right\}\cos t_0=0\\ \frac{\partial\mathcal{L}}{\partial t_1} &= \cos t_1 + \lambda(\sin t_1-\sin t_0)=0 \end{aligned}

第１式から \lambda=-1/(t_1-t_0) となり、これを第２式に代入し整理して

\displaystyle \begin{aligned} \cos t_1=\frac{\sin t_1-\sin t_0}{t_1-t_0} \end{aligned}

を得ます。この式は、 \sin t と t=t_1 で接し、 t=t_0 で交叉する直線の方程式です。下図２のように、 t=t_1 が定まると グラフから |\sin t_1-\sin t_0| を最大にする t_0 の候補 t'_0 を求めることができます

図２　 t=t_1 から t=t'_0 を求める

  まとめますと、 t=t_0 を決めると \cos t の t=t_0 での接線を描いて t=t_1 が求まり、さらに \sin t の t=t_1 での接線を描いて t=t'_0 が求まります。結局、 t_0=t'_0 となるように t=t_0 を決めれば良いことになります。この時、グラフは下図３のようになるでしょう

図３　 t_0=t'_0 のとき

図３で、紫線と緑線は (0.75\pi,0) を中心に \pi 回転させると互いに一致します。ゆえ

\displaystyle \begin{aligned} t'_0 = 1.5\pi - t_1 \end{aligned}

です。そこで、 x(t_1)=0 の条件式から t_1 を消去して整理しますと

\displaystyle \begin{aligned} 2t'_0+\cot t'_0=1.5\pi-1,\;\;\;(0\lt t'_0\lt 0.5\pi) \end{aligned}

を得ます。この式から t'_0 を求めると、 x=0 での運動エネルギーの最大値

\displaystyle \begin{aligned} K_\textrm{max}=\frac{\dot{x}^2(t_1)}{2}=\frac{1}{2}(\sin t_1-\sin t'_0)^2=2(1+\sin 2t'_0)U_p \end{aligned}

が計算でき、

\displaystyle \begin{aligned} K_\textrm{max}/U_p=2(1+\sin 2t'_0)\sim 3.17 \end{aligned}

となるはずです

計算

得られた t'_0 の条件式は、恐らく t'_0 について解析的に解くことができません。そこで、ニュートン・ラフソン法などを使って数値的に解くと

\displaystyle \begin{aligned} t'_0 = 0.313407547453934 ... \end{aligned}

を得ます。これで話を終えてしまうのは ちょっと物足りない気がしますので、悪あがきして t'_0 の近似式を求めてみようと思います。
  まず、 t'_0 の条件式の左辺を f(t'_0)=2t'_0-\cot t'_0 とおくと、その導関数 Df(t'_0) は

\displaystyle \begin{aligned} Df(t'_0)=2-\frac{1}{\sin^2t'_0} \end{aligned}

したがって、 f(t'_0) が極値をとるのは t'_0=0.25\pi の時です。増減表は

t'_0 (0) \cdots 0.25\pi \cdots (0.5\pi)
Df(t'_0) (-\infty) - 0 + (1)
f(t'_0) (\infty) \searrow 0.5\pi-1 \nearrow (\pi)

となりますが、 \pi\lt 1.5\pi -1（ t'_0 の条件式の右辺値）より、 t'_0 の解は 区間 (0, 0.25\pi) に１つだけ存在します。
  そこで、 \cot の特殊値をあげると

t'_0 \pi/12 \pi/10 \pi/8
\cot t'_0 2+\sqrt{3} \sqrt{5+2\sqrt{5}} 1+\sqrt{2}
f(t'_0) \sim 4.2556 \sim 3.7060 \sim 3.1996

t'_0=\pi/10 の時、 f(t'_0) の値が 1.5\pi-1\sim3.7124 と３桁ほど一致しています。そこで、微小量 \varepsilon をもって t'_0=\varepsilon+\pi/10 とし、 \cot を \varepsilon で展開して２次で近似しますと

\displaystyle \begin{aligned} \cot\left(\varepsilon+\frac{\pi}{10}\right)\sim \frac{1}{4}\left(\sqrt{5}+1\right)\sqrt{2\left(5+\sqrt{5}\right)} -2(3+\sqrt{5})\varepsilon+2(2+\sqrt{5})\sqrt{2(5+\sqrt{5})}\varepsilon^2 \end{aligned}

解くべき式は \varepsilon の２次方程式となります。

\displaystyle \begin{aligned} 2\sqrt{2(5+\sqrt{5})}\varepsilon^2 -2\varepsilon + \left(\sqrt{5}-2\right) \left\{\frac{1}{4}\left(\sqrt{5}+1\right)\sqrt{2\left(5+\sqrt{5}\right)}-(1.3\pi-1) \right\}= 0 \end{aligned}

２次方程式の解の公式から

\displaystyle \begin{aligned} \varepsilon = \frac{1}{2\sqrt{2(5+\sqrt{5})}} \left(1-\sqrt{1-\left(1-\frac{2}{\sqrt{5}} \right) \left\{ (5+\sqrt{5})^2-2\sqrt{10(5+\sqrt{5})}(1.3\pi-1) \right\} } \right) \end{aligned}

を得ます。実際に値を計算してみると

\displaystyle \begin{aligned} t'_0 = \varepsilon + \frac{\pi}{10} = 0.313407542 ... \end{aligned}

と、数値解と８桁目まで一致しました。最後に、ここで求まった t'_0 を 運動エネルギーの式に代入して

\displaystyle \begin{aligned} K_\textrm{max}/U_p = 3.173136550... \end{aligned}

を得ます。数値解は 3.17313656667866... で、やはり８桁目まで一致しています

重力列車の最速降下問題

重力列車の最速降下問題について、あれこれ考えてみました。

表題について

 「重力列車」とは、重力のみを推進力として移動する列車です。地表の２点（始点、終点）を結ぶ地下トンネルを掘り、レールを敷いて列車を転がします。地球の密度分布が等方的で、空気抵抗やレールとの摩擦などの非保存力を無視できる場合、重力列車は地下トンネルの形状に依らず、速度ゼロで地表の終点に到着します。

en.wikipedia.org

 「最速降下問題」とは、任意の２点を結ぶ曲線のうち、質点が最短時間で転がりきるものを求める問題です。一様重力の場合、答えはサイクロイド（擺線）となることが知られています。

en.wikipedia.org

 さて、重力列車の最速降下問題を考えると、重力の大きさと向きが場所場所で異なるため、答えはもはやサイクロイドとはなりません。ただし、始点と終点がごく近傍にある場合に限っては、重力がほぼ一様と見做せるため、答えはサイクロイドに近い曲線になろうと思われます。すると、この重力列車の最速降下曲線について次の２点が気になります：

  1. サイクロイドのように簡単な式で表すことができるか
  2. 終点に到達するまでの所要時間について、サイクロイドとの差はいかほどか

この記事の目的は、上記 1., 2. について考えることです。

一様重力における最速降下問題

まずは、一様重力における最速降下問題を考えます。この段階を踏む目的は２つあります：

  1. 単位と座標を設定する
  2. 極限 1/R \to 0 （ R は地球半径）の特別な場合として、あとで整合性のチェックに使う

問題設定

一様重力における最速降下曲線

 図のように、水平方向に x 軸、鉛直上向きに y 軸をとります。最速降下曲線は、パラメタ \theta（始点は \theta=-\pi、終点は \theta=+\pi）を使って媒介変数表示の形で求めます。座標原点は、次の式が満たされるようにとります。

\displaystyle x(+\pi) = -x(-\pi) \gt 0 \\ y(+\pi) = y(-\pi) = 0

力学的エネルギー保存則と、運動エネルギーが非負であることから、列車は始点の高さ y(-\pi) より上には登れません。よって

\displaystyle y(\theta) \leq 0

です。

最速降下曲線の方程式

列車の質量を m、重力加速度を 1 とすると、力学的エネルギー保存則から

\displaystyle \frac{m}{2}v^2 + my = 0

これを速さ v について解くと v = \sqrt{-2y} です。 所要時間 T は次の通り書けます。

\displaystyle T=\int_0^T{\textrm{d}t} = \int_{\theta=-\pi}^{\theta=+\pi} \frac{\textrm{d}l}{v} = \int_{\theta=-\pi}^{\theta=+\pi} f(y,y';x)\textrm{d}x

\textrm{d}l=\sqrt{\textrm{d}x^2+\textrm{d}y^2} は曲線の微小長さです。 x についての微分をプライム ( ') で表します。被積分関数

\displaystyle f(y,y';x) = \sqrt{\frac{1+y'^2}{-2y}}

は x に陽に依存しないので、 T が勝手な微小変形 \delta y に依らない条件はベルトラミの恒等式

\displaystyle f-y'\frac{\partial f}{\partial y'} = \frac{1}{\sqrt{-2y(1+y'^2)}} = \textrm{const.}

すなわち

\displaystyle y(1+y'^2)=\textrm{const.}

で与えられます。

en.wikipedia.org

この微分方程式は変数分離法で解くことができますが、ここでは少し趣向を変え、アタリをつけて考えてみます。

最速降下曲線の概形について考えてみる（少し脱線）

 列車にかかる重力をレールに平行／垂直な成分に分解すると、列車の加速に関わるのは平行成分のみです。特に、レールが鉛直のとき加速度最大（自由落下）、水平のとき加速度ゼロ（等速直線運動）になります。最短時間を目指すとき、次の２つがトレードオフの関係になっています：

  1. レールが急なほど、大きい加速が得られる
  2. レールが緩やかなほど、大きい 水平方向の 速度が得られる

これを踏まえると、低速な始点付近ではレールを急にして加速し、スピードがのったらレールを緩やかにして終点直下に向かって進み、最後にレールを急にして終点まで駆け上ると良さそうです（例えば、せっかちな人の車の運転：急アクセル・急ブレーキを想起してください）。すると、最速降下曲線の傾きの候補として

\displaystyle y'=\tan{\frac{\theta}{2}}

が思いつきます。

アタリをつけてみる

最速降下曲線

実際に試してみます。 y'=\tan(\theta/2) より

\displaystyle 1+y'^2=\frac{1}{\cos^2\frac{\theta}{2}}=\frac{2}{1+\cos\theta}

これをベルトラミの恒等式に代入して

\displaystyle y \propto 1+\cos\theta

を得ます。長さの単位を決めてませんでしたので、 y の最小値を -2 として

\displaystyle y = -(1+\cos\theta)

とします。すると

\displaystyle \frac{\textrm{d}x}{\textrm{d}\theta}=\frac{1}{y'}\frac{\textrm{d}y}{\textrm{d}\theta}=\frac{1}{\tan\frac{\theta}{2}}\sin\theta=\frac{\cos\frac{\theta}{2}}{\sin\frac{\theta}{2}}2\sin\frac{\theta}{2}\cos\frac{\theta}{2}=2\cos^2\frac{\theta}{2}=1+\cos\theta

となりますから、 \theta について積分して

\displaystyle x=\theta+\sin\theta

ただし、問題設定の x(\pi) = -x(-\pi) を満たすように積分定数を決めました。まとめると

\displaystyle x=\theta+\sin\theta \\ y = -(1+\cos\theta)

です。この曲線、サイクロイドは、確かにベルトラミの恒等式を満たしています。

サイクロイド

en.wikipedia.org

傾斜の変化率

あとで整合性チェックに用いるため、傾斜の変化率 y'' も求めておきます。

\displaystyle y'' = \frac{\textrm{d}}{\textrm{d}x}\left(y'\right)=\frac{1}{\textrm{d}x/\textrm{d}\theta}\frac{\textrm{d}}{\textrm{d}\theta}\left(\tan\frac{\theta}{2}\right) = \frac{1}{1+\cos\theta}\frac{\frac{1}{2}}{\cos^2\frac{\theta}{2}}= \frac{1}{(1+\cos\theta)^2}

y''>0 より、最速降下曲線は下に凸です。

所要時間 T

以上より、所要時間 T は

\displaystyle T= \int_{\theta=-\pi}^{\theta=+\pi} \sqrt{\frac{1+y'^2}{-2y}}\textrm{d}x = 2\pi

です。

 せっかくなので、１つ具体的に計算してみます。人類が到達した最深地点が「コラ半島超深度掘削坑」の約 12 \textrm{km} だそうなので、深さ 12.0 \textrm{km} のサイクロイド地下トンネルを考えます。

en.wikipedia.org

まず、サイクロイドの深さを 2 としたので、長さの 1 単位は 6.0 \textrm{km} です。次に、重力加速度を 1 とおいたことから時間の 1 単位は \sqrt{6.0\textrm{km} / (9.8\textrm{m}/\textrm{s}^2)}\sim 25\textrm{s} となります。よって所要時間は 2\pi \sim 160\textrm{s}、およそ 2 分 40 秒です。始点と終点との距離は 2\pi \sim 38\textrm{km} ですが、東京～八王子間の直線距離がおよそ 40 \textrm{km} だそうなので、すごい速さですね。

重力列車の最速降下問題

問題設定

重力列車の最速降下曲線

 座標原点で x 軸が地表に接するよう、地球中心の座標を (0, -R) とします。 y 軸は、次の式が満たされるようにとります。

\displaystyle x(+\pi) = -x(-\pi) > 0 \\ y(+\pi) = y(-\pi) > -R

極限 1/R \to 0 で、前節の問題設定と一致します。

最速降下曲線の方程式

 地球の質量を 1 とします。重力加速度を 1 とおいたため、質量 m の質点が地表で受ける重力は

\displaystyle m = G\frac{m}{R^2}

です。よって、万有引力定数は G=R^2 となります。

 地球を密度が一様な球体と考えると、中心から距離 r (\leq R) 以内の部分の質量は (r/R)^3 となります。列車が地球の中心から距離 r にあるとき、距離 r より外側の部分から受ける重力はすべて相殺されることが知られていますので、このとき列車が受ける重力 F(r) は

\displaystyle F(r) = G\frac{m(r/R)^3}{r^2} = m\frac{r}{R}

です。

赤丸の位置では、灰色部分から受ける重力はすべて相殺される

en.wikipedia.org

ゆえに、地球内部の r=\rho における位置エネルギーは、地球中心を基準として

\displaystyle -\int_\rho^0 F(r) \textrm{d}r= \frac{m}{2}\frac{\rho^2}{R}

すると、力学的エネルギー保存則から

\displaystyle \frac{m}{2}v^2 + \frac{m}{2}\frac{\rho^2}{R} = 0 + \frac{m}{2}R

これを v について解くと

\displaystyle v = \sqrt{\frac{R^2-\rho^2}{R}} = \sqrt{\frac{R^2-x^2-(y+R)^2}{R}} = \sqrt{-2y-\frac{x^2+y^2}{R}}

1/R\to 0 で v=\sqrt{-2y} となり、整合性がとれています。所要時間 T は次の通り書けます。

\displaystyle T=\int_0^T{\textrm{d}t} = \int_{\theta=-\pi}^{\theta=+\pi} \frac{\textrm{d}l}{v} = \sqrt{R}\int_{\theta=-\pi}^{\theta=+\pi} h(y,y',x)\textrm{d}x

ここで、被積分関数

\displaystyle h(y,y',x) = \sqrt{\frac{1+y'^2}{R^2-x^2-(y+R)^2}}

は残念ながら x に陽に依存しているため、オイラーの方程式

\displaystyle \frac{\partial h}{\partial y} - \frac{\textrm{d}}{\textrm{d}x}\left(\frac{\partial h}{\partial y'}\right)=0

を解かなければなりません。

en.wikipedia.org

部分ごとに分けて計算しますと、まず左辺第１項は

\displaystyle \frac{\partial h}{\partial y} = \frac{\sqrt{1+y'^2}}{\sqrt{R^2-x^2-(y+R)^2}^3}(y+R)

となります。次に、第２項で

\displaystyle \frac{\partial h}{\partial y'} = \frac{y'}{\sqrt{(1+y'^2)\left[R^2-x^2-(y+R)^2\right]}}(y+R)

なので、

\displaystyle \frac{\textrm{d}}{\textrm{d}x}\left(\frac{\partial h}{\partial y'}\right) = \frac{y''\left[R^2-x^2-(y+R)^2\right]+y'(1+y'^2)[x+(y+R)y']}{\sqrt{(1+y'^2)\left[R^2-x^2-(y+R)^2\right]}^3}

となります（しんどくなってきました）。以上をオイラーの方程式に代入すると

\displaystyle (1+y'^2)^2(y+R)-y''\left[R^2-x^2-(y+R)^2\right]-y'(1+y')[x+(y+R)y']=0

を得ます。これを展開して整理すると、次の式が得られます。

\displaystyle (1+y'^2)\left(y+R-xy'\right)+y''\left(x^2+y^2+2yR\right)=0

この微分方程式の解について、またアタリをつけて考えてみます。

最速降下曲線の概形について考えてみる（少し脱線）

最速降下曲線の方程式を R で割り

\displaystyle (1+y'^2)\left(1+\frac{y-xy'}{R}\right)+2yy''\left(1+\frac{x^2+y^2}{2yR}\right)=0

極限 1/R \to 0 をとると

\displaystyle 1+y'^2+2yy''=\frac{1}{y'}\frac{\textrm{d}}{\textrm{d}x}\left(y(1+y'^2)\right)=0

となり、一様重力の場合と整合しています。すると、式中の

\displaystyle 1+\frac{y-xy'}{R},
\displaystyle 1+\frac{x^2+y^2}{2yR}

の２つの因子が、一様重力の場合との違いそのものであることが分かります。
  ここで、第２の因子は地表

\displaystyle x^2+(y+R)^2=R^2

においてゼロになりますが、このとき最速降下曲線の方程式が満たされるには第１項がゼロでなければならず、 1+y'^2 > 0 より第１の因子がゼロとなります。 y について解けば

\displaystyle y=y'x-R

です。これは、地表における最速降下曲線の接線が地球の中心 (0, -R) を通ることを示しています。つまり、一様重力の場合と同様に、始点と終点においてレールが重力に平行になります。このことを踏まえると、レールの傾きは

\displaystyle y'=\tan\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]

となるのでは？と予想できます。
  逆に、第１の因子は地球中心を通る直線 y=y'x-R 上でゼロとなります（直線なので y'=\textrm{const.} ）が、このとき y''=0 なので方程式が満たされています。当たり前のようですが、対蹠地（地球の反対側）を結ぶ最速降下曲線は、地球中心を通る直線です。 整理すると、最速降下曲線は、

  1. 極限 1/R \to 0 でサイクロイドになる
  2. 始点と終点で、その接線が地球の中心を通る
  3. 対蹠地を結ぶとき、地球の中心を通る直線になる

ような曲線です。最も自然に思いつくのはハイポサイクロイド（内擺線）です。

アタリをつける

en.wikipedia.org

最速降下曲線

 実際に試してみます。まずハイポサイクロイドの式を求め、次に最速降下曲線の方程式に代入し、果たして１つの解になっているか確かめます。

ハイポサイクロイド

極限 1/R\to 0 で前節のサイクロイドと一致するように、転がす円の半径を 1 とします。パラメタ \theta は、図の \angle ABX です。すると、その対頂角を中心角とする円弧（黄線）の長さが \theta になります。この弧長は、転がす円が地表に接する点と O とを結ぶ円弧（緑線）の長さと等しいはずですから、この円弧に対する中心角は \angle OAB = \theta/R となります。また、直線 BX が y 軸となす角は \angle ABX - \angle OAB = (1-1/R)\theta となります。
 さて、 \vec{OX} を求めます。 \vec{OX}=\vec{OA}+\vec{AB}+\vec{BX} と分解すると、それぞれのベクトルの向き（角度）は今みた通りですから、

\displaystyle \vec{OA}=-R\hat{y}
\displaystyle \vec{AB}= (R-1)\left(\sin\frac{\theta}{R}\hat{x}+\cos\frac{\theta}{R}\hat{y}\right) \\
\displaystyle \vec{BX}=\sin\left[\left(1-\frac{1}{R}\right)\theta\right]\hat{x}-\cos\left[\left(1-\frac{1}{R}\right)\theta\right]\hat{y}

です。ただし、 \hat{x}, \hat{y} は、それぞれ x, y 軸正方向の単位ベクトルです。結局、ハイポサイクロイドの媒介変数表示は

\displaystyle x=(R-1)\sin\frac{\theta}{R}+\sin\left[\left(1-\frac{1}{R}\right)\theta\right]
\displaystyle y=(R-1)\cos\frac{\theta}{R}-\cos\left[\left(1-\frac{1}{R}\right)\theta\right]-R

となります。すると、傾き y' は

\displaystyle y'=\frac{\textrm{d}y/\textrm{d}\theta}{\textrm{d}x/\textrm{d}\theta}=\frac{\left(1-\frac{1}{R}\right)\left(\sin\frac{\theta}{R}+\sin\left[\left(1-\frac{1}{R}\right)\theta\right]\right)}{\left(1-\frac{1}{R}\right)\left(\cos\frac{\theta}{R}+\cos\left[\left(1-\frac{1}{R}\right)\theta\right]\right)}=\frac{2\cos\frac{\theta}{2}\sin\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]}{2\cos\frac{\theta}{2}\cos\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]}=\tan\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]

となり、まさに予想通りの結果となりました。
 それでは、最後に最速降下曲線の方程式にハイポサイクロイドの式を代入します。方程式を再掲します。

\displaystyle (1+y'^2)\left(y+R-xy'\right)+y''\left(x^2+y^2+2yR\right)=0

これを、４つのパートに分けて計算していきます。まず、左辺第１項について

\displaystyle 1+y'^2=\frac{1}{\cos^2\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]}

また

\displaystyle y+R-xy' \\ =(R-1)\cos\frac{\theta}{R}-\cos\left[\left(1-\frac{1}{R}\right)\theta\right]-\left((R-1)\sin\frac{\theta}{R}+\sin\left[\left(1-\frac{1}{R}\right)\theta\right]\right)\tan\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right] \\ =\frac{(R-1)\left(\cos\frac{\theta}{R}\cos\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]-\sin\frac{\theta}{R}\sin\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]\right)-\left(\cos\left[\left(1-\frac{1}{R}\right)\theta\right]\cos\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]+\sin\left[\left(1-\frac{1}{R}\right)\theta\right]\sin\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]\right)}{\cos\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]} \\ =(R-2)\frac{\cos\frac{\theta}{2}}{\cos\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]}

次に、第２項について

\displaystyle y''=\frac{\textrm{d}}{\textrm{d}x}y'=\frac{1}{\frac{\textrm{d}x}{\textrm{d}\theta}}\frac{\textrm{d}}{\textrm{d}\theta}\left(\tan\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]\right) \\ =\frac{1}{\left(1-\frac{1}{R}\right)\left(\cos\frac{\theta}{R}+\cos\left[\left(1-\frac{1}{R}\right)\theta\right]\right)}\frac{\frac{1}{2}-\frac{1}{R}}{\cos^2\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]} \\ =\frac{1-\frac{2}{R}}{1-\frac{1}{R}}\frac{1}{\left(\cos\frac{\theta}{R}+\cos\left[\left(1-\frac{1}{R}\right)\theta\right]\right)\left(1+\cos\left[\left(1-\frac{2}{R}\right)\theta\right]\right)}

これは、確かに極限 1/R\to 0 で一様重力の場合と整合しています。もう少し変形を進めて

\displaystyle y''=\frac{R-2}{R-1}\frac{1}{4\cos\frac{\theta}{2}\cos^3\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]}

次に、

\displaystyle x^2+y^2+2yR \\ =x^2+(y+R)^2-R^2 \\ =\left((R-1)\sin\frac{\theta}{R}+\sin\left[\left(1-\frac{1}{R}\right)\theta\right]\right)^2+\left((R-1)\cos\frac{\theta}{R}+\cos\left[\left(1-\frac{1}{R}\right)\theta\right]\right)^2-R^2 \\ =(R-1)^2+1-2(R-1)\left(\cos\frac{\theta}{R}\cos\left[\left(1-\frac{1}{R}\right)\theta\right]-\sin\frac{\theta}{R}\sin\left[\left(1-\frac{1}{R}\right)\theta\right]\right)-R^2\\ =-2(R-1)(1+\cos\theta)\\ =-4(R-1)\cos^2\frac{\theta}{2}

です。以上より、左辺は

\displaystyle (1+y'^2)\left(y+R-xy'\right)+y''\left(x^2+y^2+2yR\right)\\ =\frac{1}{\cos^2\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]}(R-2)\frac{\cos\frac{\theta}{2}}{\cos\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]}+\frac{R-2}{R-1}\frac{1}{4\cos\frac{\theta}{2}\cos^3\left[\left(\frac{1}{2}-\frac{1}{R}\right)\theta\right]}\left[-4(R-1)\cos^2\frac{\theta}{2}\right]\\ =0

となり、ハイポサイクロイドは最速降下曲線の方程式の１つの解であることが分かりました。

所要時間 T

以上より、所要時間 T は

\displaystyle T= \sqrt{R}\int_{\theta=-\pi}^{\theta=+\pi} \sqrt{\frac{1+y'^2}{R^2-x^2-(y+R)^2}}\textrm{d}x = 2\pi\sqrt{1-\frac{1}{R}}

となり、 1/R\to 0 の極限において一様重力の場合と一致しています。 R\sim 6400\textrm{km}に対して深さ 12 \textrm{km} 程度では 0.073 秒しか変わりません。

 一方、 R=2（最小の R）は対蹠地を結ぶ直線の場合で、このとき T=\sqrt{2}\pi となります。長さの 1 単位が 3200 \textrm{km}、時間の 1 単位が \sqrt{3200\textrm{km}/(9.8\textrm{m}/\textrm{s}^2)}\sim 570\textrm{s} となるため、所要時間は \sqrt{2}\pi\sim 2500\textrm{s}、およそ 42 分となります。

まとめ

重力列車の最速降下問題について、以下の２点を考えました。

  1. サイクロイドのように簡単な式で表すことができるか
    • 地球を密度が一様な球体と仮定した場合は、ハイポサイクロイドになる。
  2. 終点に到達するまでの所要時間について、サイクロイドとの差はいかほどか
    • 地下トンネルの深さに依る。深さ 12 \textrm{km} 程度では殆ど変わらない。

当て推量でハイポサイクロイドの式を方程式に代入したところ、なんと１つの解になっていて驚きました。ただ、調べてみると周知の事実のようでした。まあ、そうですよね ... 残念。

特殊相対性理論

特殊相対論について、自分なりに嚙み砕いた内容の備忘録です。

指導原理

特殊相対性理論の指導原理：

  1. 光速度不変の原理

    • 真空中の光速度は、どの慣性系で測定しても同一値になる

  2. 特殊相対性原理

    • すべての慣性系は等価である

固有時の導入

  いま、点光源 O を出た光が真空中を直進し、別の点 P に到達したとします。この光の速度は、光速度不変の原理の要請から、どの慣性系で測定しても同一値 c になります。従って、任意の慣性系で測定した光の変位 (\Delta x, \Delta y, \Delta z) と経過時間 \Delta t について、

\displaystyle \frac{\sqrt{(\Delta x)^2+(\Delta y)^2+(\Delta z)^2}}{\Delta t}=c

が必ず成り立ちます。そこで \Delta w = c\Delta t とおき、式を次のように変形します。

\displaystyle (\Delta w)^2 - (\Delta x)^2 - (\Delta y)^2 - (\Delta z)^2 = 0

  この式を特殊相対性原理と見比べると、 =0 は条件として強すぎるようです。すべての慣性系が等価であるためには、左辺の式の値が不変であれば十分です。そこで、質量を持つ一般の物体の慣性運動について同様に \Delta w, \Delta x, \Delta y, \Delta z を測定すると、次の式で定義される固有時 \Delta \tau が慣性系に依らない不変量になります。

\displaystyle \Delta \tau = \sqrt{(\Delta w)^2 - (\Delta x)^2 - (\Delta y)^2 - (\Delta z)^2} = \sqrt{1-v^2}\,\Delta w \tag{1}

ただし、 v = \sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2} / \Delta w は、真空中の光速度 c に対する物体の速度比です（以降、単に「速度比」と呼びます）。式(1)で、 \Delta w と速度比 v は慣性系に依りますが、固有時 \Delta \tau は慣性系に依りません。

固有時 \Delta \tau は慣性系に依らない

ローレンツ変換

  固有時が不変量であることからローレンツ変換を導出し、その帰結として、慣性運動する物体のローレンツ収縮と時間の遅れ（ウラシマ効果）を導きます。また、これらの効果が顕著に現れる有名な例として大気上層で生成されたミューオンが崩壊前に地表まで到達する現象を付録に挙げます。

導出

  式(1)の固有時 \Delta \tau は、３次元ユークリッド距離 \Delta l=\sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2} を使って

\displaystyle (\Delta w)^2 - (\Delta l)^2 = (\Delta \tau)^2

と書けます。そこで両辺を (\Delta \tau)^2 で割ると

\displaystyle \left(\frac{\Delta w}{\Delta \tau}\right)^2 - \left(\frac{\Delta l}{\Delta \tau}\right)^2 = 1

を得ます。これはまさに双曲線の方程式ですから、適当なパラメータ \theta を使って

\displaystyle \begin{align} \frac{\Delta w}{\Delta \tau} &= \cosh \theta \\\ \frac{\Delta l}{\Delta \tau} &= \sinh \theta \end{align}

と表せます。ここで、式(1)より

\displaystyle \cosh \theta = \frac{\Delta w}{\Delta \tau} = \frac{1}{\sqrt{1-v^2}}

ですから、

\displaystyle \frac{\Delta l}{\Delta \tau} = \sinh \theta = \sqrt{\cosh^2 \theta - 1} = \frac{v}{\sqrt{1-v^2}}

となります。
  以上より、基準慣性系 0 と、これに対して速度比 v で動く慣性系 1 を考えると、両者の間の変換は双曲線関数の加法定理で与えられます。

\displaystyle \begin{align} \frac{\Delta w_1}{\Delta \tau} = \cosh \theta_1 &= \cosh (\theta_0 - \theta) = \frac{1}{\sqrt{1-v^2}}\frac{\Delta w_0}{\Delta \tau} - \frac{v}{\sqrt{1-v^2}}\frac{\Delta l_0}{\Delta \tau} \\\ \frac{\Delta l_1}{\Delta \tau} = \sinh \theta_1 &= \sinh (\theta_0 - \theta) = - \frac{v}{\sqrt{1-v^2}}\frac{\Delta w_0}{\Delta \tau} + \frac{1}{\sqrt{1-v^2}}\frac{\Delta l_0}{\Delta \tau} \end{align}

添え字の 0,1 は、それぞれ慣性系 0,1 での測定量であることを表しています。最後に、分母の \Delta \tau をはらってローレンツ変換を得ます。

\displaystyle \begin{pmatrix} \Delta w_1 \\ \Delta l_1 \end{pmatrix} = \frac{1}{\sqrt{1-v^2}} \begin{pmatrix} 1 & -v \\ -v & 1 \end{pmatrix} \begin{pmatrix} \Delta w_0 \\ \Delta l_0 \end{pmatrix} \tag{2a}

逆行列をとれば、逆変換を得ます。

\displaystyle \begin{pmatrix} \Delta w_0 \\ \Delta l_0 \end{pmatrix} = \frac{1}{\sqrt{1-v^2}} \begin{pmatrix} 1 & v \\ v & 1 \end{pmatrix} \begin{pmatrix} \Delta w_1 \\ \Delta l_1 \end{pmatrix} \tag{2b}


ローレンツ収縮

  慣性系 1 上で２つの定点を考え、その間の距離を \Delta l_1 とおきます。この２点は、基準慣性系 0 上では速度比 v で移動する動点となり、その間の距離 \Delta l_0 は２点の同時刻 \Delta w_0 = 0 において測定されます。したがって、ローレンツ変換の式(2a)から

\displaystyle \Delta l_0 = \sqrt{1-v^2} \, \Delta l_1 \tag{3a}

となります。この式から、慣性運動する物体の長さについて「物体が速度比 v で動いて見える慣性系で測定される長さ \Delta l_0 は、物体が静止して見える慣性系で測定される長さ \Delta l_1 より短くなる」と言えます。このように、運動する物体が運動方向に縮んで見える現象のことを、ローレンツ収縮と呼びます。

時間の遅れ（ウラシマ効果）

  慣性系 1 上の定点で２つの時刻を計測し、その時間間隔を \Delta w_1 とおきます。慣性系 1 では点は移動しません ( \Delta l_1=0) ので、基準慣性系 0 上で測定される時間間隔 \Delta w_0 は、ローレンツ変換の式(2b)から

\displaystyle \Delta w_0 = \frac{1}{\sqrt{1-v^2}} \, \Delta w_1

すなわち

\displaystyle \Delta t_0 = \frac{1}{\sqrt{1-v^2}} \, \Delta t_1 \tag{3b}

となります。この式から、慣性運動する物体に流れる時間について「物体が速度比 v で動いて見える慣性系で測定される時間 \Delta t_0 は、物体が静止して見える慣性系で測定される時間 \Delta t_1 より長くなる」ことが分かります。すなわち、運動する物体の時間の流れは遅れて見えます。この現象は、昔話の「浦島太郎」になぞらえて、俗にウラシマ効果と呼ばれています。

付録

双曲線関数の加法定理

公式

\displaystyle \cosh (\theta_0 - \theta) = \cosh\theta\cosh\theta_0 - \sinh\theta\sinh\theta_0
\displaystyle \sinh (\theta_0 - \theta) = - \sinh\theta\cosh\theta_0 + \cosh\theta\sinh\theta_0

導出

  指数関数 \exp x を、偶関数と奇関数の和に分解します。

\displaystyle \exp x = \frac{\exp x +\exp(-x)}{2} + \frac{\exp x -\exp(-x)}{2}

右辺を見ると、偶関数の項が双曲線余弦関数 \cosh x、奇関数の項が双曲線正弦関数 \sinh x になっています。すなわち、

\displaystyle \exp x = \cosh x + \sinh x

です。これを踏まえ、指数関数 \exp (\theta_0 - \theta) を次のように展開します。

\displaystyle \begin{align} \exp (\theta_0 - \theta) &= \exp (-\theta) \, \exp \theta_0 \\ &= (\cosh \theta - \sinh \theta)(\cosh \theta_0 + \sinh \theta_0) \\ &= (\cosh \theta \cosh \theta_0 - \sinh \theta \sinh \theta_0) + (- \sinh \theta \cosh \theta_0 + \cosh \theta \sinh \theta_0) \end{align}

最後の式では、偶関数の項と奇関数の項を分けて () で括りました。最初に見た通り、偶関数の項は \cosh(\theta_0 - \theta)、奇関数の項は \sinh(\theta_0 - \theta) に相当しますので、これで双曲線関数の加法定理が導出されました。
  なお、以上の導出の流れは、オイラーの公式を利用した三角関数の加法定理の導出の流れと全く同じです。

大気上層で生成されたミューオンが崩壊前に地表まで到達する現象

  地球大気に突入した高エネルギー宇宙線は、空気中の原子と衝突して亜光速（速度比 v\sim0.995）のミューオンを生成します。このミューオンの半減期は \Delta t_{\textrm{half}}=2.20\mu\textrm{s} と非常に短く、その一部は地表まで到達する前に崩壊しますが、それでも地表では 1\textrm{cm}^2 あたり１分間に１回という高い頻度でミューオンが検出されます。
  絶対時間・絶対空間を仮定すると、これはとても奇異な事態です。なぜなら、ミューオンがその半減期の内に進む距離は

\displaystyle vc\Delta t_{\textrm{half}}\sim 0.995\cdot (3.00\times 10^8 \textrm{m/s})\cdot (2.20\times 10^{-6}\textrm{s}) \sim 0.657\text{km}

であり、地表までの距離 h_{\textrm{atm}}（ \sim 6.00\textrm{km} とします）を進む内に全体の大部分、

\displaystyle 1 - \left(\frac{1}{2}\right)^{6.00\textrm{km}/0.657\textrm{km}} \sim 99.8\%

が崩壊する計算になるためです。
  特殊相対論の効果を考えると、この問題は解消されます。ミューオンに固定した（＝ミューオンが静止して見える）慣性系で考えれば「地表までの距離のローレンツ収縮」、地表に固定した（＝地表が静止して見える）慣性系で考えれば「ミューオンの時間の遅れ（ウラシマ効果）」として説明されます。勿論、どちらの立場をとっても全く同じ結果が導かれます。

ミューオンに固定した慣性系での説明

  ミューオンに固定した慣性系では、静止するミューオンに地表が速度比 v で接近します。この時、地表までの距離はローレンツ収縮の式(3a)より

\displaystyle \sqrt{1-v^2} \, h_{\textrm{atm}} \sim \sqrt{1-0.995^2}\cdot 6.00\textrm{km} \sim 0.600\textrm{km}

まで縮みます。したがって、地表に到達するまでに崩壊するミューオンは全体の

\displaystyle 1 - \left(\frac{1}{2}\right)^{0.600\textrm{km}/0.657\textrm{km}} \sim 46.9\%

と、半分程度に過ぎません。

地表に固定した慣性系での説明

  地表に固定した慣性系では、静止する地表にミューオンが速度比 v で接近します。この時、ミューオンの寿命は時間の遅れ（ウラシマ効果）の式(3b)より

\displaystyle \frac{1}{\sqrt{1-v^2}} \, \Delta t_{\textrm{half}} \sim \frac{1}{\sqrt{1-0.995^2}} \, 2.20\mu\textrm{s} \sim 22.0 \mu\textrm{s}

まで伸びます。この間にミューオンが進む距離は、 0.995c を乗じて \sim 6.57\textrm{km} となります。したがって、地表に到達するまでに崩壊するミューオンは全体の

\displaystyle 1 - \left(\frac{1}{2}\right)^{6.00\textrm{km}/6.57\textrm{km}} \sim 46.9\%

と、半分程度に過ぎません。

相対速度（速度の合成）

  相対速度は、単純に速度ベクトルの差にはなりません。例えば、ある慣性系において x 軸上を速度 v_0, v_1 で動く２つの質点 0, 1 を考えると、質点 0 から見た質点 1 の相対速度 v_{01} は v_{01} = v_1 - v_0 とはなりません。
  実は速度 v は、 \theta を使って次のように表されます。

\displaystyle v = \frac{\Delta l}{\Delta w} = \frac{\Delta l / \Delta \tau}{\Delta w / \Delta \tau} = \frac{\sinh \theta}{\cosh \theta} = \tanh \theta

したがって、相対速度 v_{01} は双曲線正接関数の加法定理で与えられます。

\displaystyle v_{01} = \tanh (\theta_1 - \theta_0) = \frac{\tanh \theta_1 - \tanh \theta_0}{1 - \tanh \theta_1 \tanh \theta_0} = \frac{v_1 - v_0}{1 - v_1 v_0}

v_1 - v_0 に、因子 1 / (1 - v_1 v_0) がかかっていることが分かります。光速度より十分に遅い運動 (1 \gg v_0, v_1) では、この因子がほぼ１となるため、相対速度を近似的に v_1 - v_0 と考えて良いわけです。
  また、光速度 1 を速度 v で遠ざかりながら測定すると、相対速度 v_{01} は

\displaystyle v_{01} = \frac{1 - (-v)}{1 - 1 (-v)} = 1

となり、全く変わらないことが分かります。しかして光速度不変です。光速度は有限値ですが、どんな速度と合成しても変わらないという意味で、速度の無限大のように振る舞います。

３次スプライン補間 (cubic spline interpolation)

  ３次スプラインのバリエーションをまとめました。


準備

  はじめに、３次スプラインの基本を整理します。

３次スプラインの定義

  データ点 (x_0,y_0)...(x_N,y_N) を、次の区分多項式 f_j(x) で補間します。 (j=1...N)

\displaystyle f_j(x)=a_j(x-x_j)^3+b_j(x-x_j)^2+c_j(x-x_j)+d_j, \;\;\;\;\; (x_{j-1} \le x \le x_j)


ただし、 f_j(x) は以下の条件を満たします。


条件1. 区間の右側の端点でデータ点に一致。 (j=1...N)

\displaystyle f_j(x_j)=y_j


条件2. 区間の左側の端点でデータ点に一致。 (j=1...N)

\displaystyle f_j(x_{j-1})=y_{j-1}


条件3. 隣接する区間の境界点で1階微分が一致。 (j=1...N-1)

\displaystyle f'_j(x_j)=f'_{j+1}(x_j)


条件4. 隣接する区間の境界点で2階微分が一致。 (j=1...N-1)

\displaystyle f''_j(x_j)=f''_{j+1}(x_j)



図１にイメージを示します。

図１　スプライン補間のイメージ

解くべき式の導出

  上の4つの条件式を係数の組 (a_j, b_j, c_j, d_j) について解けば良いですが、これらを直接 (x_j, y_j) の式で表すことは困難です。 そこで先ず y''_j=f''_j(x_j) を使って、 (a_j, b_j, c_j, d_j) を (x_j, y_j, y''_j) の式で表します。その次に、 y''_j が満たすべき式を導きます。


[ d_j の表式 ]

条件1.より

\displaystyle f_j(x_j)=d_j=y_j

よって

\displaystyle d_j=y_j \tag{1}



[ b_j の表式 ]

f_j(x) の定義式より

\displaystyle \left.f''_j(x_j)=6a_j(x-x_j)+2b_j\,\right|_{x=x_j}=2b_j=y''_j

よって

\displaystyle b_j=\frac{y''_j}{2} \tag{2}



[ a_j の表式 ]

条件4.より

\displaystyle \left.f''_{j+1}(x_j)=6a_{j+1}(x-x_{j+1})+2b_{j+1}\,\right|_{x=x_j}=6a_{j+1}(-\Delta x_{j+1})+y''_{j+1}=y''_j

よって

\displaystyle a_j=\frac{1}{6}\frac{y''_j-y''_{j-1}}{\Delta x_j} \tag{3}


ただし、 \Delta は１つ前の項との差分を表します（ \Delta x_j=x_j-x_{j-1}）。


[ c_j の表式 ]

条件2.より

\displaystyle f_j(x_{j-1})=a_j(x_{j-1}-x_j)^3+b_j(x_{j-1}-x_j)^2+c_j(x_{j-1}-x_j)+d_j=y_{j-1}


すでに求めた係数 (a_j, b_j, d_j) の表式を代入すると

\displaystyle \frac{1}{6}\frac{y''_j-y''_{j-1}}{\Delta x_j}(-\Delta x_j)^3+\frac{y''_j}{2}(-\Delta x_j)^2+c_j(-\Delta x_j)+y_j=y_{j-1}

よって

\displaystyle c_j=s_{j-1}+\frac{1}{6}\Delta x_j(2y''_j+y''_{j-1}) \tag{4}


ただし、

\displaystyle s_j=\frac{\Delta y_{j+1}}{\Delta x_{j+1}}

としました。添字は、後の式の見栄えを良くするため、あえて１つずらしました。


[ y''_j の表式 ]

続けて y''_j が満たすべき式を導きます。条件3.より

\displaystyle f'_j(x_j)=\left.3a_j(x-x_j)^2+2b_j(x-x_j)+c_j\right|_{x=x_j}\\ =\left.3a_{j+1}(x-x_{j+1})^2+2b_{j+1}(x-x_{j+1})+c_{j+1}\right|_{x=x_j}=f'_{j+1}(x_j)

式を整理して

\displaystyle 3a_{j+1}(\Delta x_{j+1})^2-2b_{j+1}\Delta x_{j+1}+\Delta c_{j+1}=0


係数 (a_j,b_j,c_j) の表式を代入すると

\displaystyle \frac{1}{2}\frac{y''_{j+1}-y''_j}{\Delta x_{j+1}}(\Delta x_{j+1})^2-y''_{j+1}\Delta x_{j+1}+\Delta \left(s_j+\frac{1}{6}\Delta x_{j+1}(2y''_{j+1}+y''_j)\right)=0


最終的に、 y''_j の隣接３項間漸化式の形に整理できます。 (j=1...N-1)

\displaystyle \Delta x_j y''_{j-1}+2(\Delta x_j+\Delta x_{j+1})y''_j+\Delta x_{j+1} y''_{j+1}= 6\Delta s_j


行列の形で書けば

\displaystyle \begin{pmatrix} \bigcirc & \cdots & \cdots & \cdots & \cdots & \bigcirc \\ \hline \Delta x_1 & 2(\Delta x_1+\Delta x_2) & \Delta x_2 & & \huge{0} & \\ &\Delta x_2 & \ddots & \ddots & & \\ & & \ddots & \ddots & \Delta x_{N-1} & \\ & \huge{0} & & \Delta x_{N-1} & 2(\Delta x_{N-1}+\Delta x_N) & \Delta x_{N} \\ \hline \bigcirc & \cdots & \cdots & \cdots & \cdots & \bigcirc \\ \end{pmatrix} \begin{pmatrix} y''_0 \\ \vdots \\ y''_N \\ \end{pmatrix} = \begin{pmatrix} \bigcirc \\ \hline 6\Delta s_1 \\ \vdots \\ 6\Delta s_{N-1} \\ \hline \bigcirc \\ \end{pmatrix} \tag{5}


です（横線はただの仕切り線です）。

  式 (5) に示した上下２つの空白 ( \bigcirc ) の行に適当な y''_j の条件式を入れると、すべての y''_j が定まり、式 (1)-(4) から係数の組 (a_j,b_j,c_j,d_j) が求まります。このとき加える y''_j の条件式により、３次スプラインには複数のバリエーションが存在します。

３次スプラインのバリエーションと計算法

  ３次スプラインのバリエーションを挙げます。なお、周期的スプライン以外は、左端と右端とで異なるバリエーションを組み合わせることも可能です。

自然スプライン (natural spline)

  最端点 x=x_0, x_{N} で２階微分がゼロとなるように y''_j を決めます。自然スプライン曲線は、区間 [x_0, x_N] の外で直線（=２階微分がゼロ）に滑らかにつながります。

[ y''_j の条件式]

  • y''_0=y''_N=0


[ 解くべき式 ]

\displaystyle \begin{pmatrix} 1 & 0 & \cdots & \cdots & \cdots & 0 \\ \hline \Delta x_1 & 2(\Delta x_1+\Delta x_2) & \Delta x_2 & & \huge{0} & \\ &\Delta x_2 & \ddots & \ddots & & \\ & & \ddots & \ddots & \Delta x_{N-1} & \\ & \huge{0} & & \Delta x_{N-1} & 2(\Delta x_{N-1}+\Delta x_N) & \Delta x_{N} \\ \hline 0 & \cdots & \cdots & \cdots & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} y''_0 \\ \vdots \\ y''_N \\ \end{pmatrix} = \begin{pmatrix} 0 \\ \hline 6\Delta s_1 \\ \vdots \\ 6\Delta s_{N-1} \\ \hline 0 \\ \end{pmatrix}


  このような、係数行列が３重対角行列で与えられる線形連立方程式は、３重対角行列アルゴリズム（Tri-Diagonal Matrix Algorithm, TDMA）により効率的に解かれます。プログラムの実装は極めて簡単です。

固定スプライン (clamped spline)

  日本語訳が見当たらなかったので、ここでは仮に固定スプラインと呼びます。固定スプラインでは、最端点 x=x_0, x_N での１階微分の値を与えます。

\displaystyle f'_1 ( x = x_0 ) = a_1 ( - \Delta x_1 )^2+b_1( - \Delta x_1 ) + c_1 = \alpha \\ f'_N(x=x_N)=c_N=\beta


\alpha, \beta の値は任意です。 y''_j の条件式は、式(2)-(4)を代入して直ちに求まります。


[ y''_j の条件式]

  • 2\Delta x_1 y''_0+\Delta x_1 y''_1=6(s_0-\alpha)
  • 2\Delta x_N y''_N+\Delta x_N y''_{N-1}=6(\beta-s_{N-1})


[ 解くべき式 ]

\displaystyle \begin{pmatrix} 2\Delta x_1 & \Delta x_1 & 0 & \cdots & \cdots & 0 \\ \hline \Delta x_1 & 2(\Delta x_1+\Delta x_2) & \Delta x_2 & & \huge{0} & \\ &\Delta x_2 & \ddots & \ddots & & \\ & & \ddots & \ddots & \Delta x_{N-1} & \\ & \huge{0} & & \Delta x_{N-1} & 2(\Delta x_{N-1}+\Delta x_N) & \Delta x_N \\ \hline 0 & \cdots & \cdots & 0 & \Delta x_N & 2\Delta x_N \\ \end{pmatrix} \begin{pmatrix} y''_0 \\ \vdots \\ y''_N \\ \end{pmatrix} = \begin{pmatrix} 6(s_0-\alpha) \\ \hline 6\Delta s_1 \\ \vdots \\ 6\Delta s_{N-1} \\ \hline 6(\beta-s_{N-1}) \\ \end{pmatrix}


  ここでも係数行列が３重対角行列になっており、３重対角行列アルゴリズムが有効です。

ノットなしスプライン (not-a-knot spline)

  ノット（節点）とは、隣接する区間の曲線が互いに結合する点（データ点）のことです。ノットなしスプラインでは、 x=x_1,x_{N-1} で３階微分が連続になるように y''_j を決めます。自然スプラインや固定スプラインと異なり、最端点 x=x_0, x_N での１階、２階微分の値を指定しません。

\displaystyle f'''_1 ( x = x_1 ) = 6a_1 = 6a_2 = f'''_2 ( x = x_1 ) \\ f'''_{N-1}(x=x_{N-1}) = 6a_{N-1} = 6a_N = f'''_N(x=x_{N-1})


最端点での１階、２階微分の値が不明な場合、ノットなしスプラインが有用です。

  ノットなしスプラインでは、 x=x_1,x_{N-1} で０～３階微分がすべて連続になるため、 f_1(x) と f_2(x)、 f_{N-1}(x) と f_N(x) はそれぞれ全く同じ関数になります。つまり、見かけ上 x=x_1,x_{N-1} のノットが消失します。 y''_j の条件式は、式(3)を代入して直ちに求まります。


[ y''_j の条件式]

  • \Delta x_2 y''_0 - (\Delta x_1 + \Delta x_2) y''_1 + \Delta x_1 y''_2 = 0
  • \Delta x_N y''_{N-2} - (\Delta x_{N-1} + \Delta x_N) y''_{N-1} + \Delta x_{N-1} y''_N = 0


[ 解くべき式 ]

\displaystyle \begin{pmatrix} \Delta x_2 & -(\Delta x_1+\Delta x_2) & [\Delta x_1] & 0 & \cdots & 0 \\ \hline \Delta x_1 & 2(\Delta x_1+\Delta x_2) & \Delta x_2 & & \huge{0} & \\ &\Delta x_2 & \ddots & \ddots & & \\ & & \ddots & \ddots & \Delta x_{N-1} & \\ & \huge{0} & & \Delta x_{N-1} & 2(\Delta x_{N-1}+\Delta x_N) & \Delta x_N \\ \hline 0 & \cdots & 0 & [\Delta x_N] & -(\Delta x_{N-1}+\Delta x_N) & \Delta x_{N-1} \\ \end{pmatrix} \begin{pmatrix} y''_0 \\ \vdots \\ y''_N \\ \end{pmatrix} = \begin{pmatrix} 0 \\ \hline 6\Delta s_1 \\ \vdots \\ 6\Delta s_{N-1} \\ \hline 0 \\ \end{pmatrix}


[ ] で囲った要素により、係数行列が３重対角行列になっていません。第２行の \Delta x_1 / \Delta x_2 倍を第１行から引き、第 N 行の \Delta x_N / \Delta x_{N-1} 倍を第 (N+1) 行から引くことで、[ ] で囲った要素を消去します。適当に定数倍して式を整えると、


\displaystyle \begin{pmatrix} \Delta x_1-\Delta x_2 & 2\Delta x_1+\Delta x_2 & 0 & \cdots & \cdots & 0 \\ \hline \Delta x_1 & 2(\Delta x_1+\Delta x_2) & \Delta x_2 & & \huge{0} & \\ &\Delta x_2 & \ddots & \ddots & & \\ & & \ddots & \ddots & \Delta x_{N-1} & \\ & \huge{0} & & \Delta x_{N-1} & 2(\Delta x_{N-1}+\Delta x_N) & \Delta x_N \\ \hline 0 & \cdots & \cdots & 0 & 2\Delta x_N+\Delta x_{N-1} & \Delta x_N-\Delta x_{N-1} \\ \end{pmatrix} \begin{pmatrix} y''_0 \\ \vdots \\ y''_N \\ \end{pmatrix} = \begin{pmatrix} 6\frac{\Delta s_1}{1+\Delta x_2 / \Delta x_1} \\ \hline 6\Delta s_1 \\ \vdots \\ 6\Delta s_{N-1} \\ \hline 6\frac{\Delta s_{N-1}}{1+\Delta x_{N-1} / \Delta x_N} \\ \end{pmatrix}


を得ます。これで、３重対角行列アルゴリズムを使える形になりました。

＜注意＞
  \Delta x_1-\Delta x_2 = 0 または \Delta x_N-\Delta x_{N-1} = 0 の場合、３重対角行列アルゴリズムをそのまま適用するとゼロ除算が起きます。この場合は、 y''_1, y''_{N-1} についてそれぞれ独立に解けますので、これらを消去してから適用します。

\displaystyle \begin{pmatrix} \hline \Delta x_1 & \Delta x_2 & & & & \\ 0 & 2(\Delta x_2+\Delta x_3) & \Delta x_3 & & \huge{0} & \\ &\Delta x_3 & \ddots & \ddots & & \\ & & \ddots & \ddots & \Delta x_{N-2} & \\ & \huge{0} & & \Delta x_{N-2} & 2(\Delta x_{N-2}+\Delta x_{N-1}) & 0 \\ & & & & \Delta x_{N-1} & \Delta x_N \\ \hline \end{pmatrix} \begin{pmatrix} y''_0 \\ y''_2 \\ \vdots \\ y''_{N-2} \\ y''_N \\ \end{pmatrix} = \begin{pmatrix} \hline 6\Delta s_1 -2(\Delta x_1+\Delta x_2)y''_1 \\ 6\Delta s_2 -\Delta x_2y''_1 \\ 6\Delta s_3 \\ \vdots \\ 6\Delta s_{N-3} \\ 6\Delta s_{N-2} -\Delta x_{N-1}y''_{N-1}\\ 6\Delta s_{N-1} -2(\Delta x_{N-1}+\Delta x_N)y''_{N-1}\\ \hline \end{pmatrix}


\displaystyle y''\_1 = 6\frac{\Delta s_1}{1+\Delta x_2 / \Delta x_1}\frac{1}{2\Delta x_1+\Delta x_2}
\displaystyle y''_{N-1} = 6\frac{\Delta s_{N-1}}{1+\Delta x_{N-1} / \Delta x_N}\frac{1}{2\Delta x_N+\Delta x_{N-1}}


  上記の場合以外で、 \Delta x_1-\Delta x_2 または \Delta x_N-\Delta x_{N-1} が 0 に近い場合は、計算が不安定になると思われます。この場合は、ガウスの掃き出し法など、別のアルゴリズムを使った方が良いかもしれません。

周期的スプライン (periodic spline)

  周期的スプラインでは、両最端点 x=x_0, x_N での１階、２階微分の値が互いに一致するように y''_j を決めます。 y_0=y_N であれば、スプライン曲線は区間 [x_0,x_N] の外に周期的に繋がります。

\displaystyle f'_1(x=x_0) = 3a_1(-\Delta x_1)^2+2b_1(-\Delta x_1)+c_1 = c_N = f'_N(x=x_N) \\ f''_1(x=x_0) = 6a_1(-\Delta x_1)+2b_1 = 2b_N = f''_N(x=x_N)


y''_j の条件式は、式(2)-(4)を代入して直ちに求まります。


[ y''_j の条件式]

  • 2\Delta x_1 y''_0+\Delta x_1 y''_1+\Delta x_N y''_{N-1}+2\Delta x_N y''_N=6(s_0-s_{N-1})
  • y''_0-y''_N=0


[ 解くべき式 ]

\displaystyle \begin{pmatrix} 2\Delta x_1 & \Delta x_1 & 0 & \cdots & 0 & \Delta x_N & 2\Delta x_N \\ \hline \Delta x_1 & 2(\Delta x_1+\Delta x_2) & \Delta x_2 & & & \huge{0} & \\ &\Delta x_2 & \ddots & & \ddots & & \\ & & \ddots & & \ddots & \Delta x_{N-1} & \\ & \huge{0} & & & \Delta x_{N-1} & 2(\Delta x_{N-1}+\Delta x_N) & \Delta x_N \\ \hline 1 & 0 & \cdots & \cdots & \cdots & 0 & -1 \\ \end{pmatrix} \begin{pmatrix} y''_0 \\ \vdots \\ y''_N \\ \end{pmatrix} = \begin{pmatrix} 6(s_0-s_{N-1}) \\ \hline 6\Delta s_1 \\ \vdots \\ 6\Delta s_{N-1} \\ \hline 0 \\ \end{pmatrix}


３重対角行列アルゴリズムを適用するために変形を行います。第 (N+1) 行の 2\Delta x_N 倍を第 1 行、 \Delta x_N 倍を第 N 行に加えます。このとき、第 (N+1) 行の式 y''_0 - y''_N=0 を別に書くと、解くべき式は次の通りになります。

\displaystyle \begin{pmatrix} 2(\Delta x_N+\Delta x_1) & & \Delta x_1 & 0 & \cdots & 0 & & [\Delta x_N] \\ \hline \Delta x_1 & & 2(\Delta x_1+\Delta x_2) & \Delta x_2 & & & \huge{0} & \\ & & \Delta x_2 & \ddots & & \ddots & & \\ & \huge{0} & & \ddots & & \ddots & & \Delta x_{N-1} \\ [\Delta x_N] & & & & & \Delta x_{N-1} & & 2(\Delta x_{N-1}+\Delta x_N) \\ \hline \end{pmatrix} \begin{pmatrix} y''_0 \\ \vdots \\ y''_{N-1} \\ \end{pmatrix} = \begin{pmatrix} 6(s_0-s_{N-1}) \\ \hline 6\Delta s_1 \\ \vdots \\ 6\Delta s_{N-1} \\ \hline \end{pmatrix} \\


\displaystyle y''\_0 - y''\_N=0


右上と左下の角に非ゼロの要素（[ ] で囲った要素）がありますが、これも３重対角行列アルゴリズムを適用できる形です。例えば、次のWikipediaのページ ("Variants") を参照。

en.wikipedia.org


各バリエーションの比較テスト

自然スプライン、固定スプライン、ノットなしスプライン

  FORTRANで即席のプログラムを作成しました。SPLINE_INT() を呼び出して係数を決定したのち、SPLINE() を呼び出して区間 [x_0, x_N] の任意の点を計算します。また、SPLINE_INT() では、左端と右端とで別々に３次スプラインの種類を指定します。


"input1.txt" からデータ点を読み取ってスプライン補間し、結果を "spline.txt" に出力します。ここでは次の適当なデータ点で試してみます。


"input1.txt"

0.2   0.4392
0.7   0.8638
1.6   0.5449
2.3   0.2019
3.0   0.0190
4.0  -0.0374


  補間の結果を、下の図２に示します。

図２　３次スプライン補間の計算結果

固定スプラインの結果は、最端点 x=0.2, 4.0 でやや無理な傾きを指定しているため (\alpha=-1, \beta=1)、自然スプラインとノットなしスプラインの結果に比べて大きくたわんでいます。一方、自然スプラインとノットなしスプラインの結果の差は、図の左側で大きくなっているように見えます。最左端 x=0.2 の付近を拡大してみます。

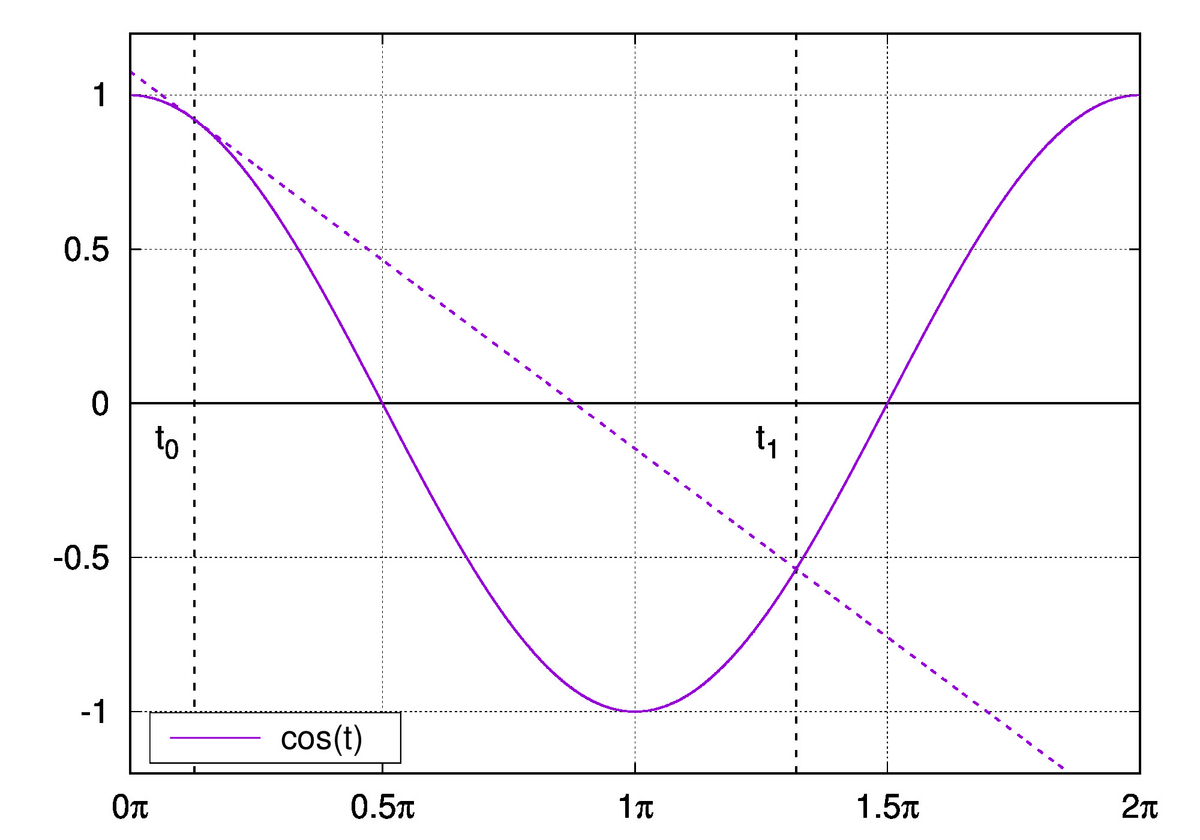
図３　左端点付近の拡大図。接線との比較

  図３では、 x=0.2 での接線を点線で描き加えました（係数が分かっているので、当然接線を求めることができます）。 x が増加したときの接線との乖離の程度を見比べると、明らかに自然スプラインの方が直線に近い形をしていることが分かります。

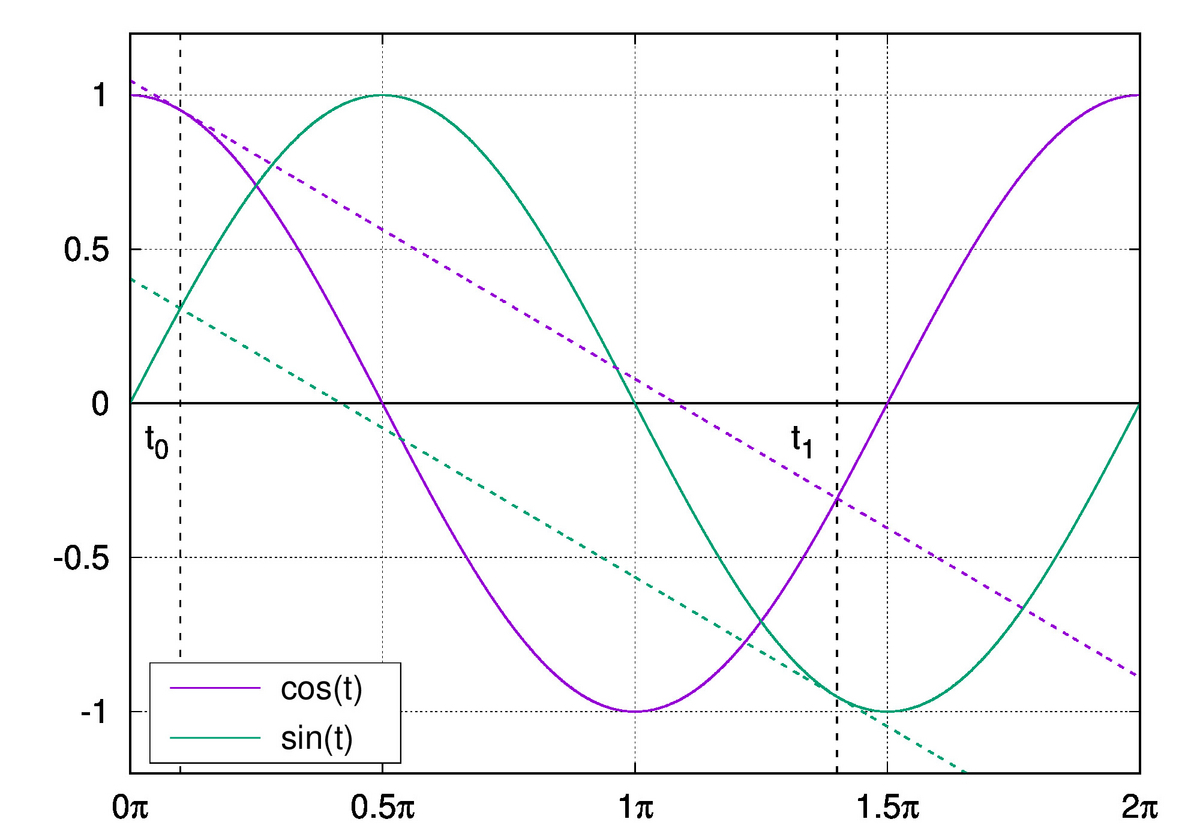
図４　最左端付近の拡大図。 f_1(x) との比較

  図４では、 f_1(x) を点線で描き加えました。自然スプラインは x\gt x_1 で乖離していますが、一方でノットなしスプラインは x\gt x_2 で乖離しています。見かけ上 x=x_1 のノットが消失していることが分かります。

周期的スプライン

  FORTRANで即席のプログラムを作成しました。SPLINE_INT() を呼び出して係数を決定したのち、SPLINE() を呼び出して区間 [x0,xN] の任意の点を計算します。


"input2.txt" からデータ点を読み取ってスプライン補間し、結果を "splineP.txt" に出力します。ここでは次の適当なデータ点 (y=\sin x) で試してみます。


"input2.txt" 

0.7854   0.7071
1.0472   0.8660
1.5708   1.0000
2.0944   0.8660
2.3562   0.7071
2.6180   0.5000
3.1416  -0.0004
3.6652  -0.5000
3.9270  -0.7071
4.1888  -0.8660
4.7124  -1.0000
5.2360  -0.8660
5.4978  -0.7071
5.7596  -0.5000
6.2832   0.0000
6.8068   0.5000
7.0686   0.7071


  補間の結果を、下の図５に示します。

図５　周期的スプラインによる周期関数の補間

補間を行った区間は、中央の縦線 (x=2.25\pi) より左側です。右側の曲線は、左側の補間の結果を１周期ずらしてプロットしたものです。１階微分を破線、２階微分を点線であわせて示しました。いずれも、縦線のところで滑らかにつながっています。

  比較のため、自然スプライン、固定スプライン、ノットなしスプラインによる補間の結果を示します。

図６　自然スプラインによる周期関数の補間

  図６は自然スプラインの結果です。実線の結果は悪くないように見えますが、１階微分は明らかに不連続です。２階微分は、最端点でゼロになる条件に無理があり、縦線の付近で不自然な振る舞いをしています。

図７　固定スプラインによる周期関数の補間

  図７は固定スプラインの結果です。両最端点での１階微分は、どちらも \sin'(2.25\pi) =1/\sqrt{2} としました。１階、２階微分とも滑らかにつながっているように見えます（実際に滑らかにつながっている訳ではありません）。最端点での１階微分の値が予め分かっているため、それらしい結果が得られました。

図８　ノットなしスプラインによる周期関数の補間

  図８はノットなしスプラインの結果です。１階微分まで滑らかにつながっているように見えます（実際に滑らかにつながっている訳ではありません）。２階微分は明らかに不連続ですが、自然スプラインの結果と比べると、こちらの結果の方が無理がありません。


まとめ

  ３次スプラインの４つのバリエーションをまとめました。また、即席のプログラムで実際にスプライン補間を行い、それぞれの特徴を見ました（表１）。

表１　３次スプラインのバリエーション
周期的スプライン 両最端点の１階、２階微分の値を互いに一致させる。
周期的なデータの補間に適する。
自然スプライン最端点での２階微分の値をゼロとする。
直線で無理なく補外できるデータの補間に適する。
固定スプライン最端点での１階微分の値を指定する。
最端点での傾きが分かっているデータの補間に適する。
ノットなしスプライン 最端点での条件を指定しない。
一般的なデータの補間に用いられる。